열심히 코딩 하숭!
[알고리즘] 힙(Heap) | 개념정리 및 구현 방법 본문
힙(Heap)
우선순위큐를 구현하는 데 주로 사용되는 트리 기반 자료구조
특정 규칙에 따라 부모 노드와 자식 노드 간의 관계가 정해져 있어,
효율적으로 최대값이나 최소값을 빠르게 찾을 수 있다
힙의 특징
[완전 이진 트리]
힙은 항상 완전 이진트리의 형태를 유지함
항상 왼쪽에서 오른쪽으로 순차적으로 채워지며, 마지막 레벨만 부분적으로 채울 수 있음 (차곡차곡)
[최대 힙]
부모 노드의 값이 자식 노드보다 항상 크거나 같음
[최소 힙]
부모 노드의 값이 자식 노드의 값보다 항상 작거나 같음

힙의 구조
트리 구조이지만 배열로 구현되는 경우가 많음!
완전 이진 트리 구조이기 때문에, 배열 인덱스만으로 부모와 자식 노드를 효율적으로 찾을 수 있다
- 부모 노드 인덱스: i
- 왼쪽 자식 인덱스: 2i + 1
- 오른쪽 자식 인덱스: 2i + 2
- 부모 노드 인덱스 (역으로 찾기): (i - 1) // 2
구현을 쉽게 하기 위해, 첫번째 인덱스인 0은 사용되지 않는다.
특정 위치의 노드번호는 새로운 노드가 추가되어도 변하지 않는다.

힙 삽입 (Insertion)
(1) 힙에 새로운 요소가 들어오면, 우선 새로운 노드를 힙의 제일 마지막 노드에 이어서 삽입한다
(2) 새로운 노드를 부모 노드들과 교환시키면서 힙의 성질을 만족하도록 한다 (상향 조정(Heapify-Up))
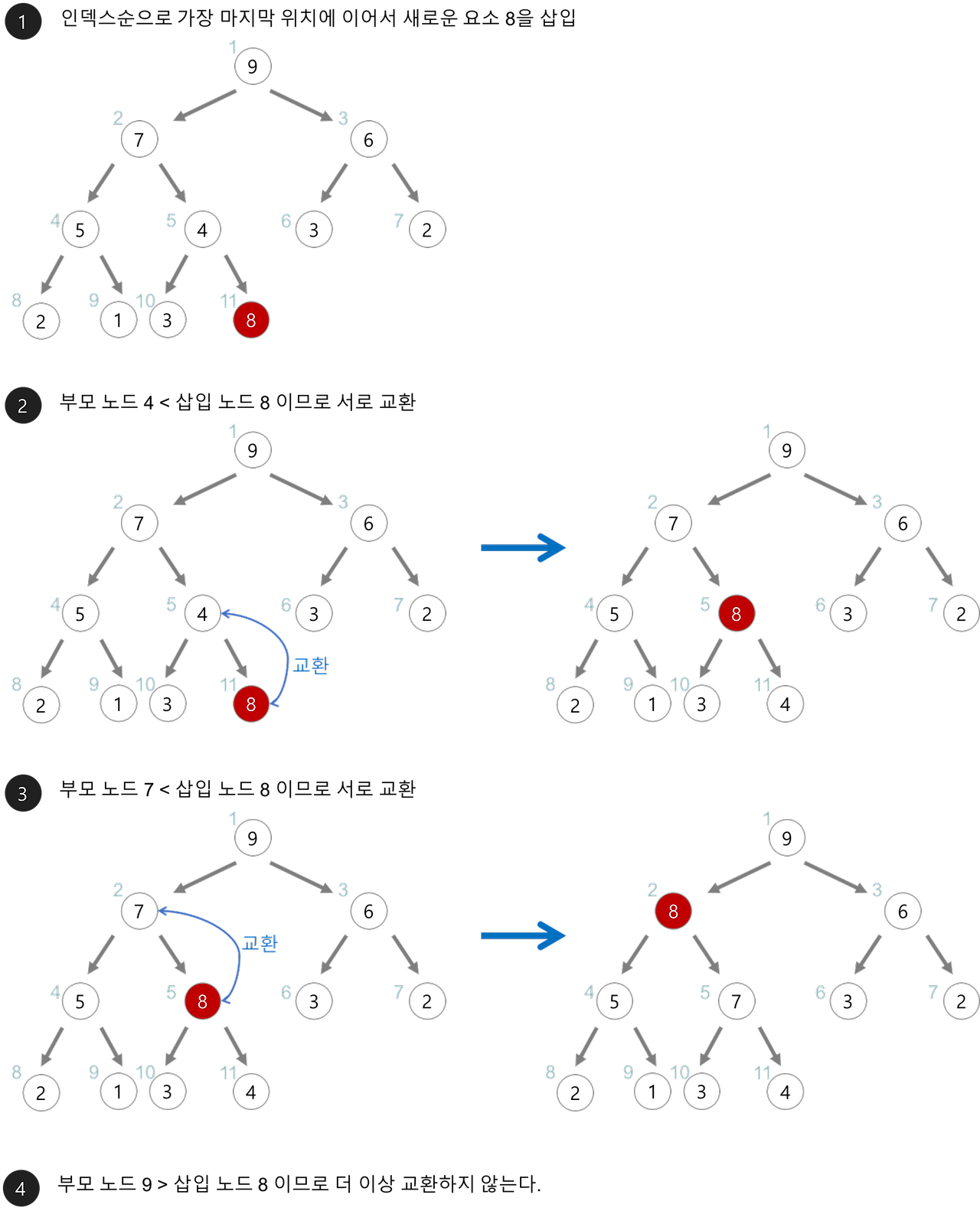
* 주의: 같은 레벨의 자식노드들 끼리의 크기는 중요하지 않다!!! 위아래만 보면 된다.
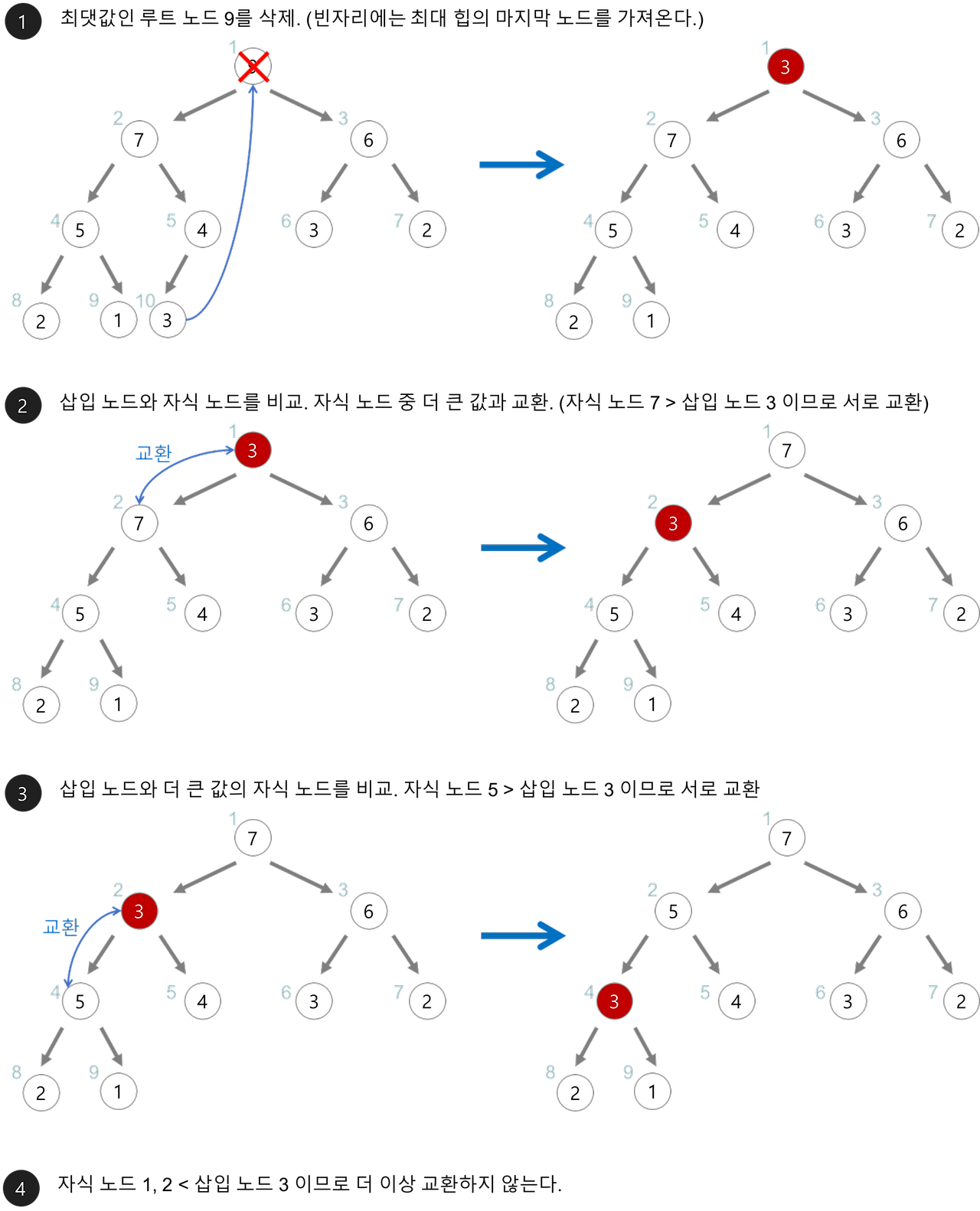
힙 삭제 (Deletion)
(1) 최대 힙에서 최대값은 루트 노드이므로 루트 노드가 삭제된다 (최소힙에서는 최소값인 루트노드가 삭제됨)
(2) 삭제된 루트노드에는 마지막 노드를 가져온다
(3) 힙을 재구성한다 (하향 조정(Heapify-Down))
힙 시간 복잡도
삽입: O(logn)
삭제: O(logn)
* 삽입, 삭제 자체는 O(1)로 가능하지만, heapify과정에서 O(logn) 소요
최대값/최소값 조회: O(1)
python으로 heap 문제 풀기
heapq 라이브러리를 사용함! (최소힙임! 최대힙을 구현하려면, 값을 음수로 바꾸고 진행해야 함)
- heapify(list): 리스트를 힙으로 변환 (O(n))
- heappush(heap, item): 힙에 요소 추가 (O(log n))
- heappop(heap): 힙에서 최소값 제거 및 반환 (O(log n))
- heappushpop(heap, item): 새 값을 추가한 뒤 최소값을 제거하고 반환 (O(log n))
- heapreplace(heap, item): 최소값을 제거한 뒤 새 값을 추가 (O(log n))
import heapq
heapq.heapify(nums) # 리스트를 최소힙으로 만듦
heapq.heappush(nums, 1) # 값 추가
heapq.heappop(nums) # nums 중 가장 최소값 하나를 pop
heapq.heappushpop(nums, 1) # 값 추가한 뒤, 최소값을 제거하고 반환
# -> 얘는 새로 추가된 값이 제거될 수도 있음
heapq.heapreplace(nums, 1) # 최소값 제거한 뒤 새 값 추가
# 얘는 최소값을 제거하면서 새 값을 반드시 유지해야 할 때 씀
# 최소값 확인 (제거하지 않음)
min_value = heap[0]
직접 구현하면 아래와 같다!
def heapify(arr, n, i):
largest = i # 현재 루트 노드
left = 2 * i + 1 # 왼쪽 자식
right = 2 * i + 2 # 오른쪽 자식
# 왼쪽 자식이 더 크면 갱신
if left < n and arr[left] > arr[largest]:
largest = left
# 오른쪽 자식이 더 크면 갱신
if right < n and arr[right] > arr[largest]:
largest = right
# 루트 노드가 자식 노드보다 작으면 스왑
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
# 재귀적으로 하위 트리를 힙화
heapify(arr, n, largest)
def heap_sort(arr):
n = len(arr)
# 힙 구성
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# 정렬
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 루트 노드와 끝 노드 스왑
heapify(arr, i, 0) # 힙 속성 유지
# 테스트
data = [3, 6, 5, 0, 8, 2, 1, 9]
heap_sort(data)
print("Sorted:", data)
출처
chatGPT 답변
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 재귀함수 | 재귀 문제를 풀 때의 접근법... (1) | 2024.12.04 |
|---|---|
| [알고리즘] 2470 두 용액 | baekjoon 문제 풀이 (0) | 2023.04.07 |
| [알고리즘][정렬] 10815번 숫자 카드 | baekjoon 문제 풀이 (0) | 2023.04.03 |
| [알고리즘][정렬] 10814번 나이순 정렬 | baekjoon 문제 풀이 (0) | 2023.04.03 |
| [알고리즘][DP, 수학] 2839번 설탕 배달 | baekjoon 문제 풀이 (0) | 2023.04.02 |



