열심히 코딩 하숭!
2022 하천 분리수거 마라톤 대회 '시뮬레이션 프로그램🏃' | Red Black Tree | 자료구조실습 중간과제 본문
2022 하천 분리수거 마라톤 대회 '시뮬레이션 프로그램🏃' | Red Black Tree | 자료구조실습 중간과제
채숭이 2022. 10. 22. 00:07
네이버 블로그에 써두었던 글인데 티스토리에도 남기면 좋을 것 같아서 올리게 되었다!
* 학교에서 수강 중인 22-2 '자료구조 실습' 수업의 중간 프로젝트에 대한 글이다.
0. 프로젝트 개요
1) 자료구조에 사용될 데이터 수집 : “하천 쓰레기”
- 이번 프로젝트의 주제는 "하천 쓰레기" 였다. 휴대폰을 사용해 하천에 떠있는 쓰레기 사진을 찍는다.
- 쓰레기 사진은 다음과 같이 csv 파일로 정리한다.

2) 데이터를 사용해 해결할 수 있는 새로운 문제 정의
- 수집한 데이터를 이용해 지금까지 배운 자료구조로 해결해볼 수 있는 문제를 정의한다.
3) 문제 접근 방법 제시
- 자료구조를 이용해 문제를 해결하는 방법에 대해 간단히 제시한다.
1. 데이터 수집
서울 성동구에 있는 서울숲과 서울 성북구에 있는 성북천에서 하천 쓰레기 사진을 찍었고 총 102장의 사진이 데이터로 수집되었다.



그 후, 사진의 특성에 따라 이를 csv 파일로 정리하였다.
파일에는 다음과 같은 정보가 들어가게 된다.
|
Name
|
Widths
|
Hights
|
Latitude
|
Longitude
|
Rubbish
|
Plastics
|
Cans
|
Glass
|
Papers
|
|
사진의 이름
|
사진의 가로(pixel)
|
사진의 세로(pixel)
|
장소의위도
|
장소의 경도
|
일반쓰레기 유무
|
플라스틱 유무
|
캔 유무
|
유리 유무
|
종이 쓰레기 유무
|
|
string
|
int
|
int
|
double
|
double
|
bool (0/1)
|
bool (0/1)
|
bool (0/1)
|
bool (0/1)
|
bool (0/1)
|
아래는 직접 정리한 csv 파일의 일부를 캡쳐한 것이다.

장소가 성북천 / 서울숲으로 한정되었다보니 사진끼리 경도, 위도 값이 유사한 것을 확인할 수 있었고, 하천 쓰레기는 일반쓰레기와 플라스틱의 개수가 가장 많은 것을 확인해볼 수 있었다.
2. 문제 정의
2022 하천 분리수거 마라톤 대회를 개최한다!!!

대회 정보
대회명 | 2022 하천 분리수거 마라톤
접수기간 | 2022년도 11월 15일 ~ 11월 25일
참가비 | 무료
대회기간 | 2022년도 12월 19일(월), 20일(화)
상품 | 1등 아이패드 / 2등 애플워치 / 참가상 텀블러
유의사항
1. 참가자는 출발 지점과 도착 지점을 지정합니다. (5km ~ 30km로 제한)
2. 도착 지점까지 마라톤을 하며 지정한 곳의 하천 쓰레기를 주워야 합니다.
3. 각 쓰레기는 가산점으로 환산됩니다. (일반 쓰레기 – 4점, 플라스틱 - 6점, 캔 – 4점, 유리 – 5점, 종이 – 4점)
4. 가산점 계산 어플을 통해 가산점과 경로를 계산할 수 있습니다
설명
하천을 생각하는 환경 마라톤이 개최되었다. 참가자들은 5~30km 이내의 거리를 선택하여 마라톤을 하며 하천에 있는 쓰레기를 줍는다. 주워야하는 쓰레기는 데이터 사진 촬영 과정을 통해 수집되었던 하천 쓰레기로 한정된다. 쓰레기의 종류마다 해당하는 가산점이 있고, 총 가산점이 높은 참가자 순으로 등수를 매기게 된다.
가산점은 아래의 표와 같다.
|
일반 쓰레기
|
플라스틱
|
캔
|
유리
|
종이
|
|
4점
|
6점
|
4점
|
5점
|
4점
|
🏃 마라톤 시뮬레이션 프로그램 ⭐
대회 참가자들은 마라톤을 하기 전, 본인의 가산점과 마라톤 거리를 계산해보고 싶어한다. 마라톤 참가자는 프로그램에 원하는 만큼 시작과 끝 지점을 입력한 후 입력받은 구간들이 5km ~ 30km이내인지, 가산점은 몇 점인지, 가산점의 최대값과 그 때의 경로는 무엇인지, 시간은 얼마나 걸리는지 등을 출력받을 수 있다.
3. 마라톤 시뮬레이션 프로그램에 사용하는 자료구조 & 해결 방법
1) 데이터 관리 - Red Black Tree
먼저, 데이터 관리에 사용될 자료구조인 Red Black Tree를 선택한 이유에 대해 설명하도록 하겠다.
이진 탐색 트리(BST Tree)는 트리의 높이만큼의 연산이 수행된다는 특징이 있기 때문에 높이가 줄어들수록 실행 시간이 짧아지게 된다. 그러나 최악의 경우 높이와 노드의 수가 같아지는 상황이 벌어지게 되고 이는 곧 리스트와 같아져 매우 비효율적인 연산이 수행된다.
이를 개선하기 위해 등장한 것이 AVL Tree인데 AVL Tree는 left node의 height와 right node의 height 차가 1이라 높이를 매우 획기적으로 줄일 수 있다는 장점이 있지만 rebalanced를 위한 rotation 시간이 오래 걸린다는 단점이 있다.
이러한 BST와 AVL Tree의 단점을 개선하는 것이 Red Black Tree이다. Red Black Tree는 이진 탐색 트리의 모든 특징을 가지고 있고 추가적으로 다음과 같은 규칙을 따른다.
- 모든 노드는 Red 또는 Black으로 색칠되어있다.
- root 노드는 Black이다.
- 모든 leaf 노드는 Black이다.
- 노드가 Red일 경우 그 자식 노드들은 모두 Black이다.
- 각 노드로부터 그 노드의 자손인 leaf 노드로 가는 경로 사이에 있는 Black 노드의 수는 모두 같다.
해당 규칙들로 인해 Red Black Tree는 root 노드로부터 가장 먼 leaf 노드까지의 높이가, root 노드로부터 가장 가까운 leaf 노드까지의 높이의 2배 보다 항상! 작다. 그리고 AVL tree 보다 더 적은 횟수로, 적당히 균형을 맞추게 되기 때문에 연산 시간이 줄어들어 비교적 효과적이다.

Red Black Tree (c++) 🎄
GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
(코드는 해당 깃허브를 참고하고 읽어보았다)
2) Red Black Tree 사용 시 유의사항
Red Black Tree에 하천 쓰레기 사진이 가지고 있는 정보 중 사진 이름과 크기를 제외한 모든 정보를 node에 입력할 것인데, 이 때 *위도를 기준*으로 값들을 insert할 것이다. insert 시, 다음과 같은 유의사항을 지켜가며 insert 해야 한다.
유의사항 1. 한정 거리 계산
- 만약 트리에 삽입되어 있는 데이터와의 위도 값 차이가 0.4도 이상이거나 경도 값 차이가 0.5도 이상이면 마라톤의 거리 기준을 넘어선 것으로 판단하고 insert 하지 않는다.
ㄴ 위도: 1도 - 약 111 km
ㄴ 위도 0.4도의 경우 40km 이상의 거리이므로 매우 멀어 마라톤 불가
ㄴ 경도: 1도 - 약 88 km (대한민국 기준)
ㄴ 경도 0.5도의 경우 40km 이상의 거리이므로 매우 멀어 마라톤 불가
유의사항 2. insert하려는 노드와 다른 노드의 위도는 동일하지만 경도는 다를 경우
- 경도를 기준으로 하여, 새로 insert하려는 노드의 경도 값이 위도가 동일한 노드의 경도 값보다 작을 경우 새 노드를 왼쪽으로 이동시키고, 경도 값이 클 경우 오른쪽으로 이동시킴
유의사항 3. insert하려는 노드와 다른 노드의 위도, 경도가 모두 동일할 경우
- 쓰레기 종류의 여부까지 같다면) insert하지 않는다.
ㄴ 위도 경도가 동일하고 쓰레기 종류의 여부까지 같을 경우 같은 데이터의 중복이라고 판단한다.
- 쓰레기 종류의 여부가 다르다면) insert 대신, 해당 노드의 데이터 값만 변경한다.
ㄴ 예를 들어, 일반쓰레기만 1이었던 노드에 접근하여 플라스틱 쓰레기의 여부 또한 1로 변경한다.
3) 경로 조사 및 가산점 계산 - 중위 순회
참가자가 원하는 출발지와 도착지를 설정하게 되면 search 함수를 사용하여 출발지 노드를 찾는다. 그 후 도착지 노드가 나오기 전까지 중위 순회를 진행하며 노드의 가산점을 합산하고, 위도 경도 값을 활용하여 예상 거리를 계산한다.
여기서 중위 순회란 left - mid - right 순으로 방문하는 순회 방법이고 Red Black Tree를 중위 순회하게 될 경우 오름차순 된 키 값을 얻을 수 있다.
그리고 거리 계산의 경우 경도, 위도 값을 사용할 것이고 소수점 둘째자리까지 반영된 값이므로 정확하지는 않지만 대략적인 거리 계산은 할 수 있을 것으로 기대된다. 계산 시 아래와 같은 위도, 경도 정보를 이용한다.
|
위도
|
경도 (우리나라 기준)
|
|
1도 - 111.195 km
1분 - 1.853 km
1초 - 30.887m
|
1도 - 88.804 km
1분 - 1.408 km
1초 - 24.668 m
|
(참고 | 1분 = 1도/60 등분, 1초 = 1분/60 등분)
4) 최종 순위 - 참가자 class를 이용해 객체 선언
참가자가 입력하는 만큼 참가자 객체를 선언하여 계산된 각각의 가산점, 거리 등을 정보로 입력한 후 객체 간의 비교를 통해 순서를 매긴다.
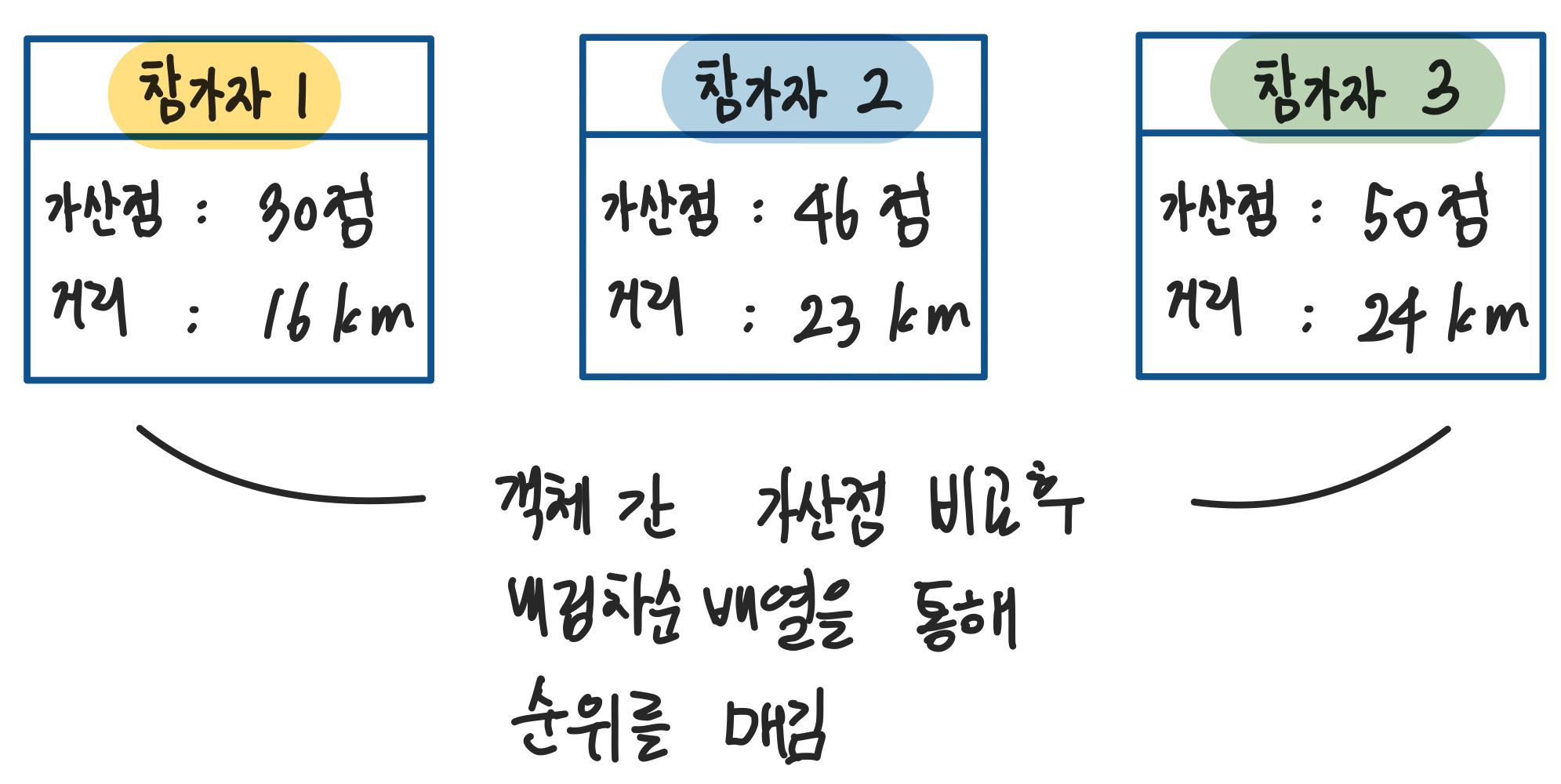
기말 프로젝트 때 해당 프로그램을 C++을 이용해 직접 구현하도록 하겠다.
아자아자!
사진 및 CSV 파일 데이터는 아래의 구글 드라이브를 통해 다운로드 받을 수 있습니다. (수강생을 제외한 타인의 사용 금지)
https://drive.google.com/drive/folders/1Iy35k_yciR_sHj6ciWhVUmGUJOGzIPVQ?usp=sharing
22-2 자료구조실습 - 하천 쓰레기 IMG - Google Drive
이 폴더에 파일이 없습니다.이 폴더에 파일을 추가하려면 로그인하세요.
drive.google.com
'학교 과제 > 2022-2 자료구조실습 과제' 카테고리의 다른 글
| Kruskal, Prim, Dijkstra 알고리즘 | 자료구조실습 12주차 과제 (0) | 2022.11.27 |
|---|---|
| BFS vs DFS | 자료구조실습 9주차 과제 (0) | 2022.11.06 |
| AVL tree | 자료구조실습 4주차 과제 (0) | 2022.10.02 |
| 이진 탐색 트리 | 자료구조실습 3주차 과제 (0) | 2022.09.25 |
| 우선순위큐 & 힙 | 자료구조실습 2주차 과제 (1) | 2022.09.18 |




