열심히 코딩 하숭!
AVL tree | 자료구조실습 4주차 과제 본문
* 성신여대 22-2학기 자료구조실습 수업시간에 배운 내용을 토대로 요약 정리한 글입니다
1. Data structures augmentation 코딩
1) Rank 구현
- Rank(t) : (How many Scheduled) ≤ t
- 스케줄링 문제에서 가게에 손님이 왔을 때 지금 물품이 몇 개나 예약 되어 있는지, 재료가 얼마나 더 필요한지 등을 나타낼 때 이를 Rank라고 칭함
- 이후 남은 재료수 : |x| - Rank(t) (여기서 |x|는 총 개수)
- 스케줄링 문제의 경우 3주차 과제 글을 참고 | https://chaesoong2.tistory.com/12
- 구하는 방법
- Array로 구현할 경우) index가 곧 Rank(t)가 됨
- Binary Search Tree의 경우) subtree 개수 + 본인 개수를 통해 구할 수 있음

예를 들어, Rank(50)을 구하려면 (x는 50)
1) 42 -> x보다 작으므로 1을 더하고 42의 왼쪽 노드의 subtree 개수인 4를 더해준다 (누적 값: 5)
2) 42보다 x의 값이 더 크기 때문에 오른쪽으로 내려간다
3) 67-> x보다 크므로 1을 더하고 왼쪽 노드의 subtree 개수인 1을 더해준다 (누적 값:7)
4) 왼쪽으로 내려간다
5) x == 50 이므로 연산을 종료한다
-> BST 문제에서 약간의 변화만 주면 해결할 수 있음! (노드 클래스에서 subtree 개수 추가, 알고리즘 변경 등)
하지만, BST가 balanced 하지 않을 경우 list와 비슷해져 비효율적인 결과를 불러올 수 있음
2) AVL tree 구현
Balanced한 BST를 구현하기 위해 나온 것이 AVL tree이다
- 수업에서 나온 문제
S = {40, 17, 22, 1, 7, 8, 18, 9, 50, 29, 23, 90, 99, 107, 100, 15, 80, 25, 20,31} (총 20개의 key값)
해당 노드들을 이진트리로 나타내는 대신 다음의 조건을 만족시켜라.
조건 1_ 왼쪽 자식의 높이와 오른쪽 자식의 높이의 차가 1이도록 하여라.
조건 2_전체 트리의 h(높이)가 min일 때와 max일 때를 각각 구해라
- 나의 답안
min
일단 오름차순으로 key 값들을 나열하고 노드가 완성될 때까지 계속 중앙값을 찾아가며 트리에 중앙값을 넣었다. (level_min = 4)
max
처음에는 root의 왼쪽, 오른쪽 자식만 생각하면 되는 줄 알고 쭉 나열하여 20을 정답으로 외쳤었는데, 그게 아니었다. (level_max = 10)
- 해답
min
나의 해답과 같았다. 중앙값을 찾으며 최대한 트리를 꽉꽉 채워가면 된다. (level_min = 4)
max
거의 모든 노드에서 [왼쪽 subtree 높이] = [오른쪽 subtree 높이] 일 경우
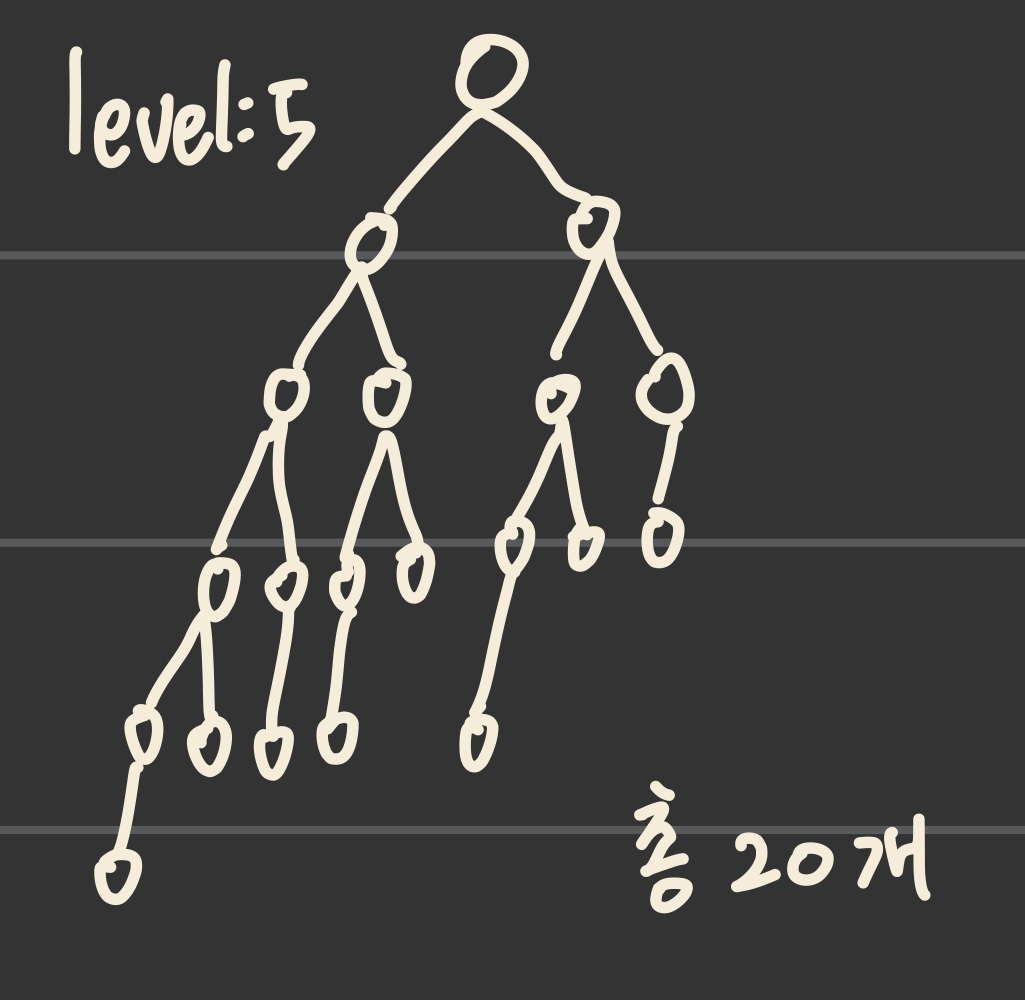
(level_max = 5)
h의 min과 max의 차이가 매우 근소함 => BST가 balanced하지 않은 문제를 해결할 수 있다!
2. AVL tree 정의 등 강의 내용 정리
1) AVL tree의 정의
- AVL tree란
[왼쪽 자식의 높이]와 [오른쪽 자식의 높이]의 차가 1 또는 0
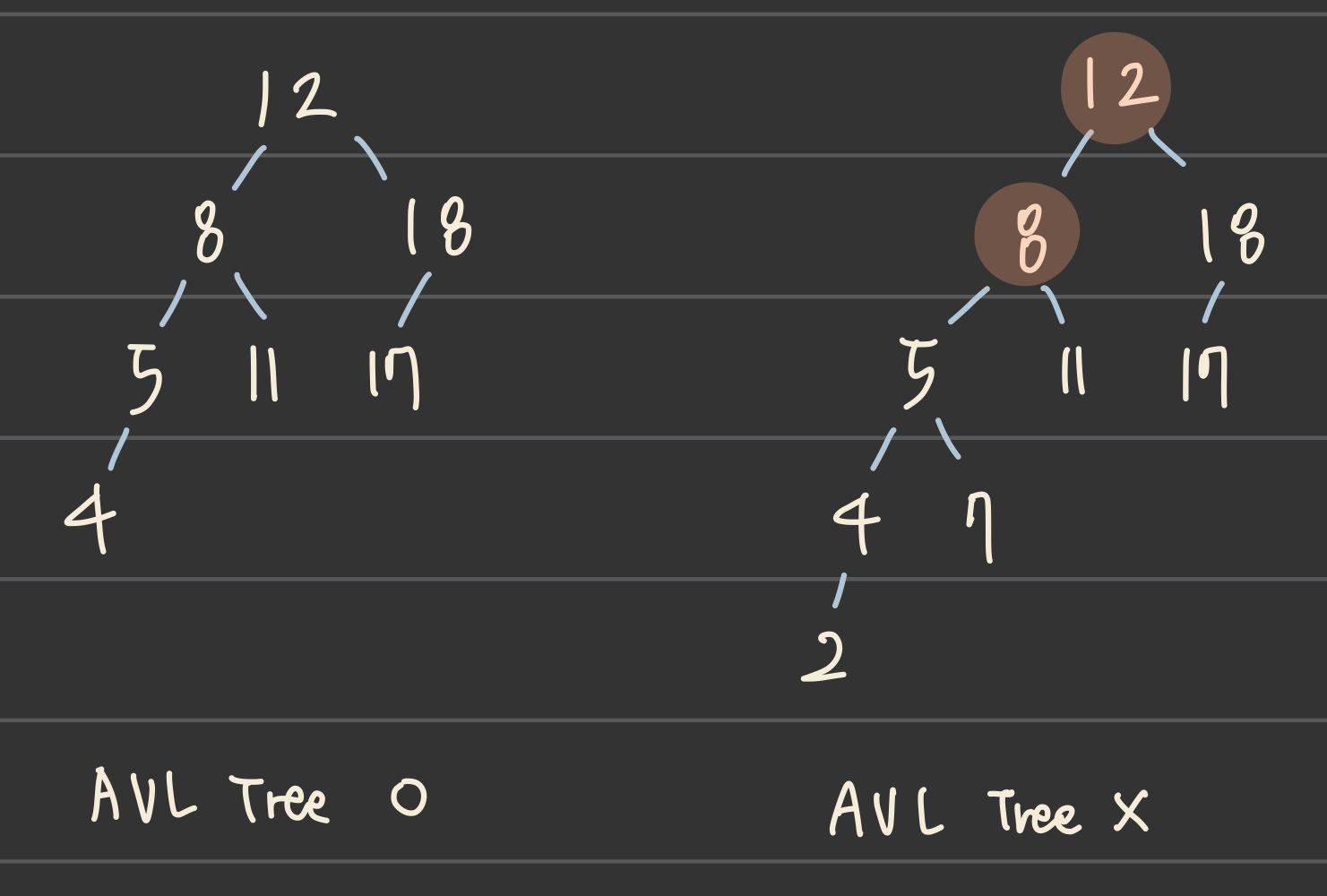
- Big-O
시간복잡도를 O(N)에서 O(logN)으로 줄임
항상 O(logN)을 보장함
2) insert 연산
삽입의 경우 BST와 동일하게 삽입 연산을 해주면 되는데,
(BST 삽입 연산은 아래의 글의 BinSrchTree 클래스의 insert 함수를 참고)
https://chaesoong2.tistory.com/12
이때 트리에 불균형이 나타나게 될 경우 트리의 높이 조절을 위한 rotate이 필요하다.
기본 rotation에는 left rotation과 right rotation이 있다.

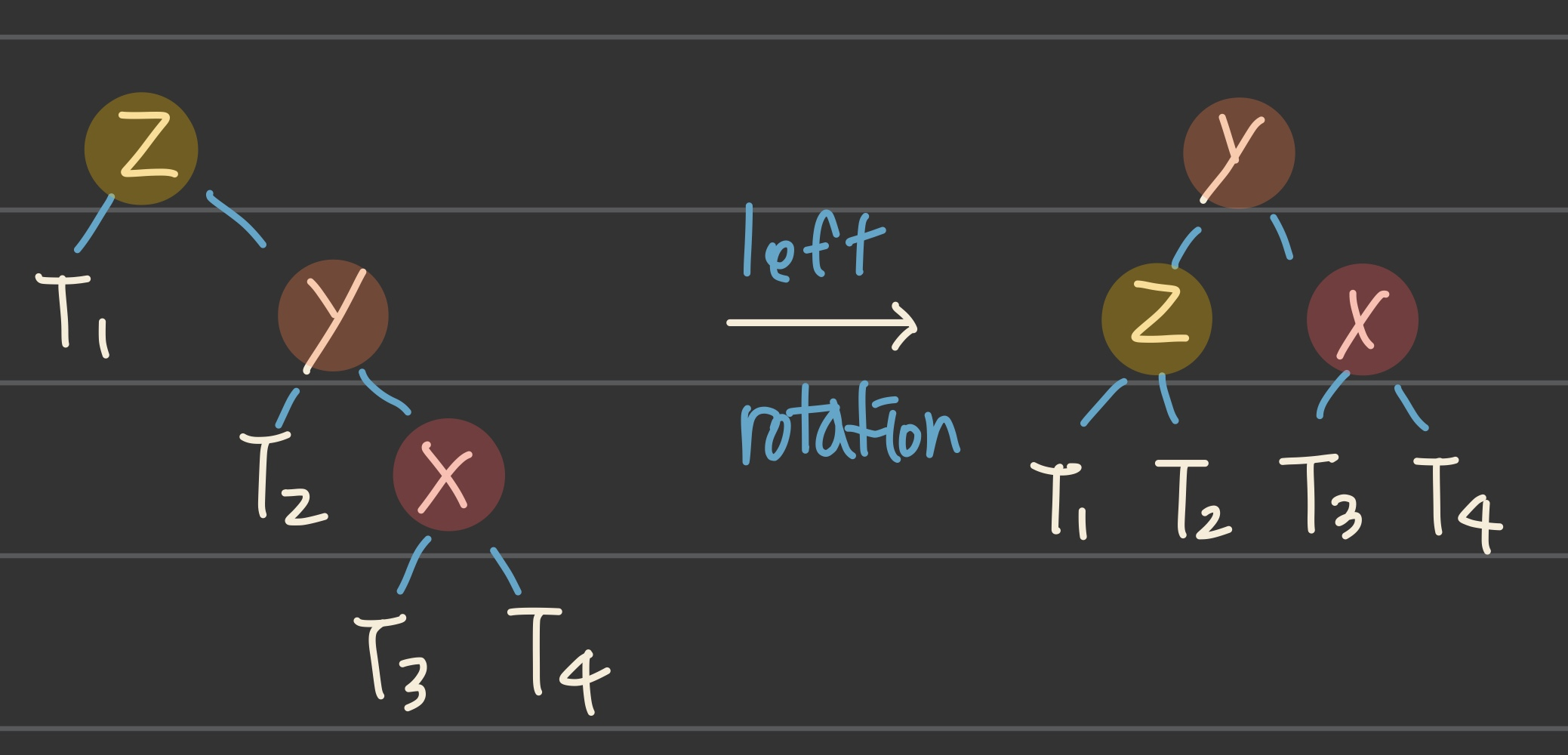
left rotation은 오른쪽 subtree가 높아서 불균형이 발생할 때
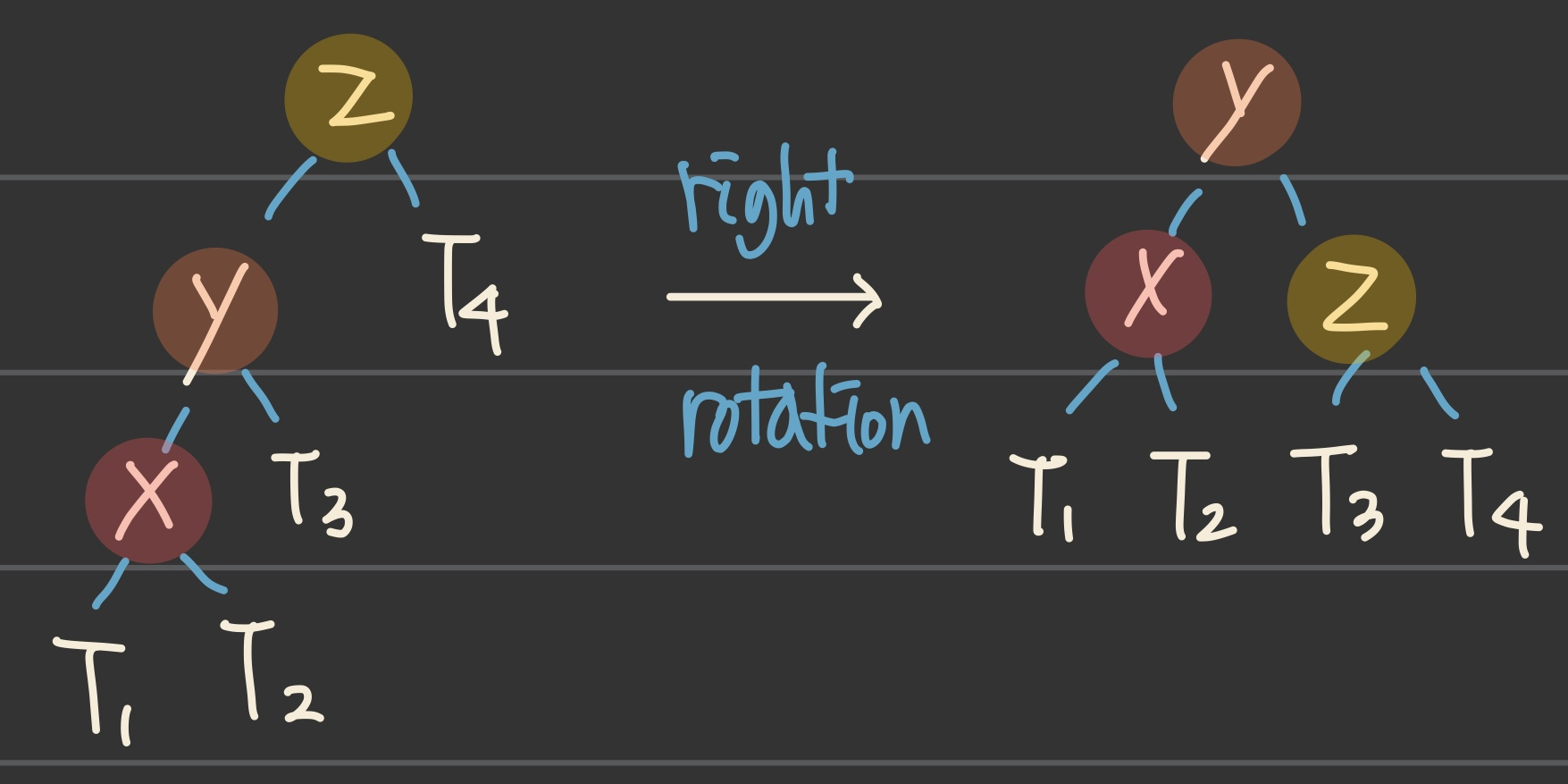
right rotation은 왼쪽 subtree가 높아서 불균형이 발생할 때 사용한다
z를 삽입한다고 할 때, rotation이 발생하는 경우는 다음과 같은 네 가지의 case로 나누어 볼 수 있다.
① LL
- 트리가 왼쪽으로 치우친 경우
=> right rotate
② RR
- 트리가 오른쪽으로 치우친 경우
=> left rotate
③ LR
- 왼쪽 자식 노드에 오른쪽 자식 노드만 있을 경우
=> left rotate & right rotate
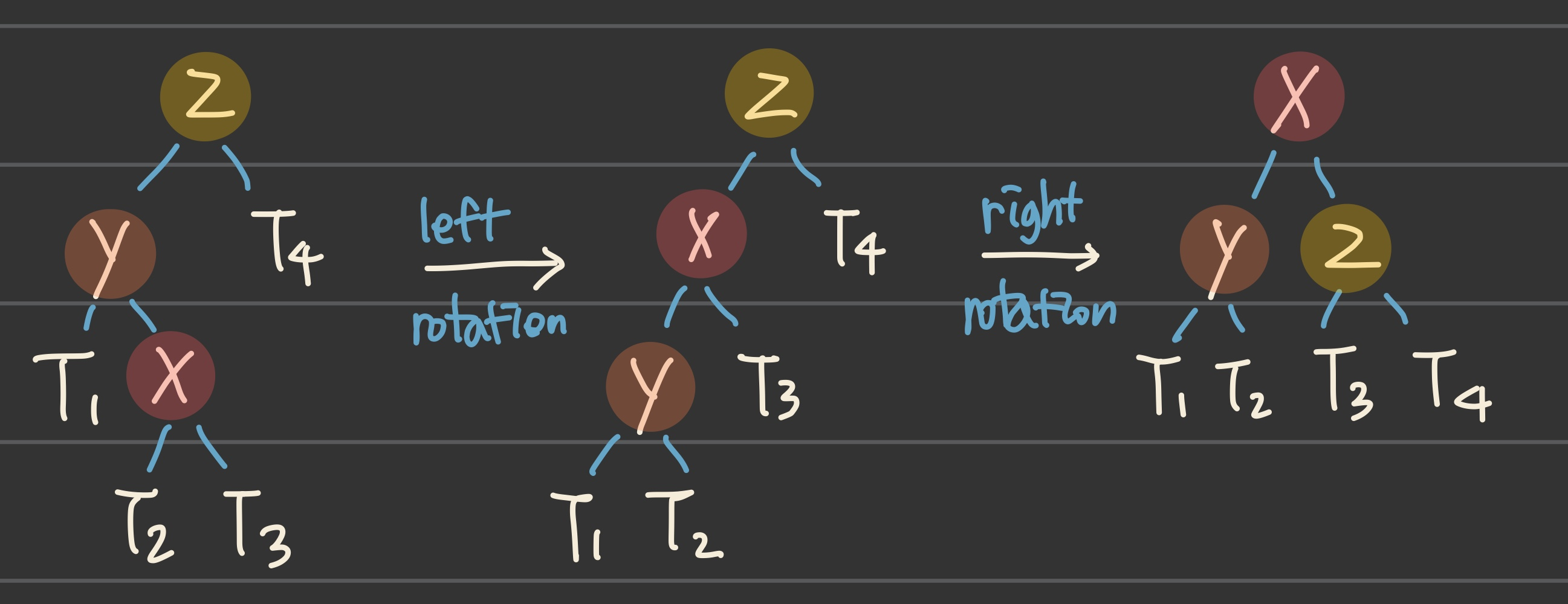
④ RL
- 오른쪽 자식 노드에 왼쪽 자식 노드만 있을 경우
=> right rotate & left rotate
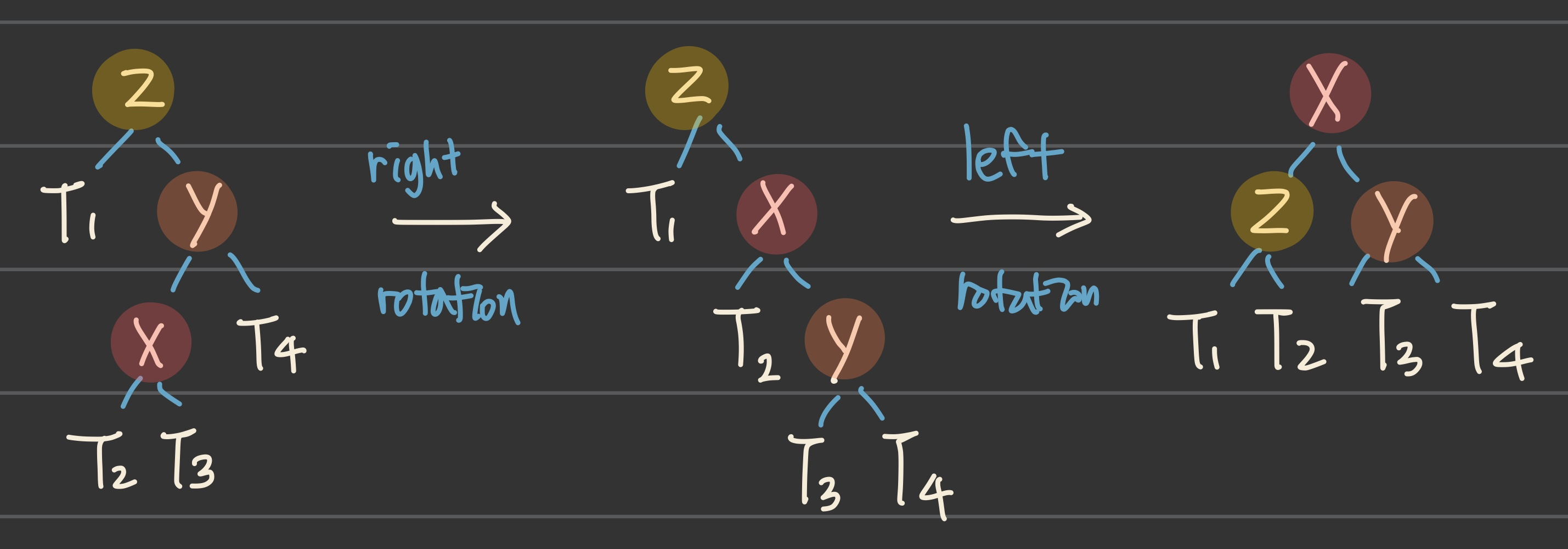
위와 같은 방법으로 불균형을 해결하면 된다.
3) delete 연산
delete 연산의 경우
우선 먼저 BST에서와 같이 삭제 연산을 수행해주고
(BST 삭제 연산은 아래의 글의 BinSrchTree 클래스의 remove 함수를 참고)
https://chaesoong2.tistory.com/12
삭제 후에 불균형이 생기면 위의 insert에서 처럼 rotation을 통해 불균형을 해결해주면 된다
*Geeks for geeks 개념 정리 내용을 보고 작성함
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
https://www.geeksforgeeks.org/avl-tree-set-2-deletion/
코드 참고
https://jaimemin.tistory.com/275
3. Leet code 문제 풀이
# 110. Balanced Binary Tree
https://chaesoong2.tistory.com/13
110. Balanced Binary Tree | LeetCode 문제 풀이
https://leetcode.com/problems/balanced-binary-tree/ Balanced Binary Tree - LeetCode Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepar..
chaesoong2.tistory.com
'학교 과제 > 2022-2 자료구조실습 과제' 카테고리의 다른 글
| BFS vs DFS | 자료구조실습 9주차 과제 (0) | 2022.11.06 |
|---|---|
| 2022 하천 분리수거 마라톤 대회 '시뮬레이션 프로그램🏃' | Red Black Tree | 자료구조실습 중간과제 (0) | 2022.10.22 |
| 이진 탐색 트리 | 자료구조실습 3주차 과제 (0) | 2022.09.25 |
| 우선순위큐 & 힙 | 자료구조실습 2주차 과제 (1) | 2022.09.18 |
| 프로젝트를 위한 시각 넓히기 | The SDGs 2021을 읽고 | 14. 해양 생태계 (0) | 2022.09.12 |




