분류, 결정트리, Overfitting | 3주차 - 5 | 파이썬 머신러닝 완벽가이드

* 해당 글은 inflearn의 강의 '[개정판] 파이썬 머신러닝 완벽가이드'를 정리한 글입니다.

 

 

 

회색 - 강의 제목

노란색, 주황색 - 강조

 

 

 

---

 

5일

 

 

분류(Classification) 개요와 결정트리(Decision Tree) 소개

 

 

분류 알고리즘 (Classification)

- 주어진 데이터의 피처와 레이블값을 학습해서 모델 생성

- 생성된 모델에 새로운 데이터 값이 주어졌을 때, 미지의 값을 예측

 

결정 트리 개요

- 매우 쉽고 유연하게 적용될 수 있음

- 데이터의 스케일링이나 정규화 등의 사전 가공의 영향이 적음

- 예측 성능 향상을 위해 복잡한 규칙 구조를 가져야 하며, 이로 인해 과적합(overfitting)이 발생해 반대로 예측 성능이 저하될 수도 있다는 단점이 있음

 

 

앙상블 기법 개요

- 결정 트리의 단점이 앙상블 기법에서는 오히려 장점으로 작용함

- 매우 많은 여러개의 약한 학습기(== 예측 성능이 상대적으로 떨어지는 학습 알고리즘)를 결합해서 확률적 보완과 오류가 발생한 부분에 대한 가중치를 계속 업데이트하면서 예측 성능을 향상시킴 (이 때 결정트리가 좋은 약한 학습기가 된다)

- GBM, XGBoost, LightGBM 등

 

 

 

결정 트리

- 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내서 트리 기반의 분류 규칙을 만든다

- ∴ 어떤 기준을 바탕으로 규칙을 만들어야 가장 효율적인 분류가 될 것인가가 알고리즘의 성능을 크게 좌우함

 

균일도 측정 방법

 

방법 1. 정보 이득(Information Gain)

- 정보 이득 지수 = 1 - 엔트로피 지수

- 엔트로피: 주어진 데이터 집합의 혼잡도, 다른 정보들이 더 많이 섞여있을 수록 엔트로피는 커짐

- 정보 이득 지수가 높을수록 데이터의 혼잡도가 낮음

  ∴  정보 이득이 높은 속성을 기준으로 분할함!

 

방법 2. 지니 계수

-  0이 가장 평등하고, 1로 갈수록 불평등함

- 불평등: 데이터가 균일하지 못 하다

- 지니 계수가 작을 수록 정보의 균일도가 높음

 

 

규칙 노드 생성 프로세스

 

결정 트리의 특징

장점

- 쉽다. 직관적이다.

- 피처의 스케일링이나 정규화 등의 사전 가공 영향도가 크지 않다

단점

- 과적합으로 알고리즘 성능이 떨어진다. → 이를 극복하기 위해 트리의 크기를 사전에 제한하는 튜닝이 필요

 

 

 

 

결정트리 모델 시각화를 위한 Graphviz 설치하기

 

 

Graphviz

- 이용하면 결정 트리 모델을 시각화 할 수 있음

 

설치

- Graphviz 실행 파일 설치

- Graphviz 파이썬 래퍼 모듈 설치

- OS 환경변수 구성

 

 

 

 

시각화를 통한 결정 트리 모델의 구조 이해

 

 

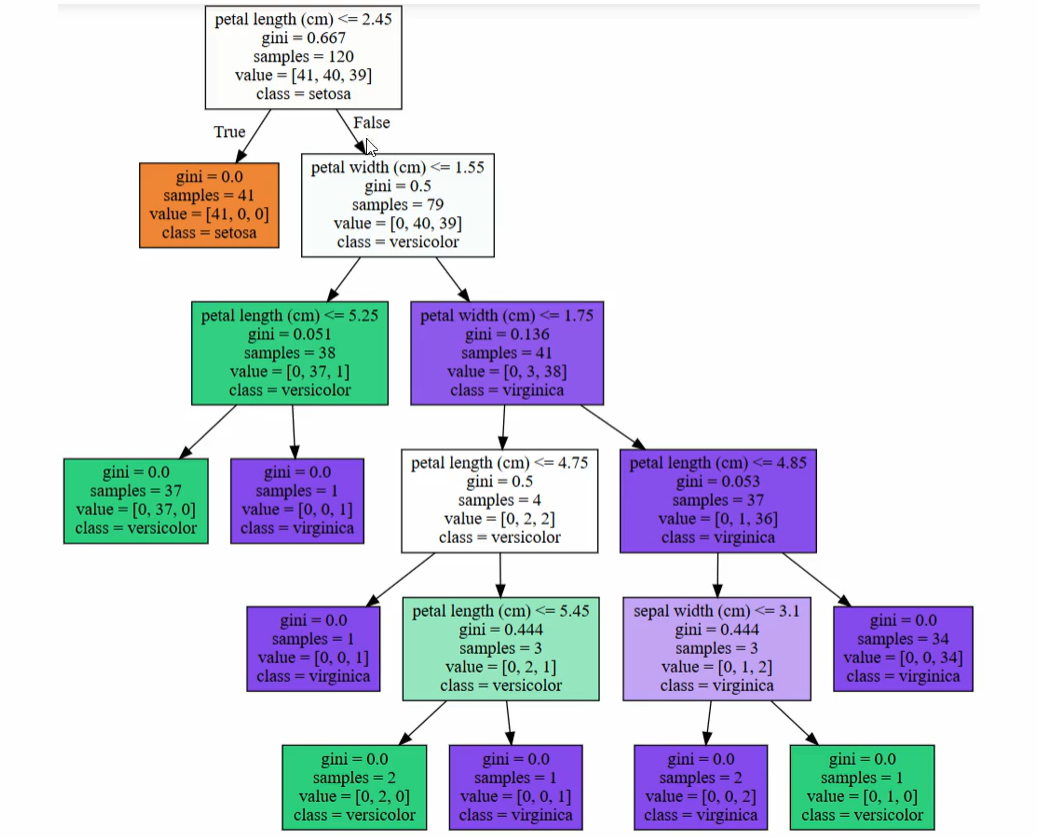
Graphviz의 시각화 노드 설명

- petal length <= 2.45 → 자식 노드를 만들기 위한 규칙 조건 (조건이 없으면 리프노드임 or 클래스 하나의 값만 남을 경우 리프 노드임) - gini → value로 주어진 데이터 분포에서의 지니 계수 - samples → 현 규칙에 해당하는 데이터 건수 - value = [41, 40, 39] → 클래스 값 기반의 데이터 건수 (순서대로 0,1,2) - class → value 리스트 내에서 가장 많은 건수를 가진 결정값

 

 

 

결정 트리 주요 하이퍼 파라미터의 이해

 

 

결정 트리 주요 하이퍼 파라미터

 

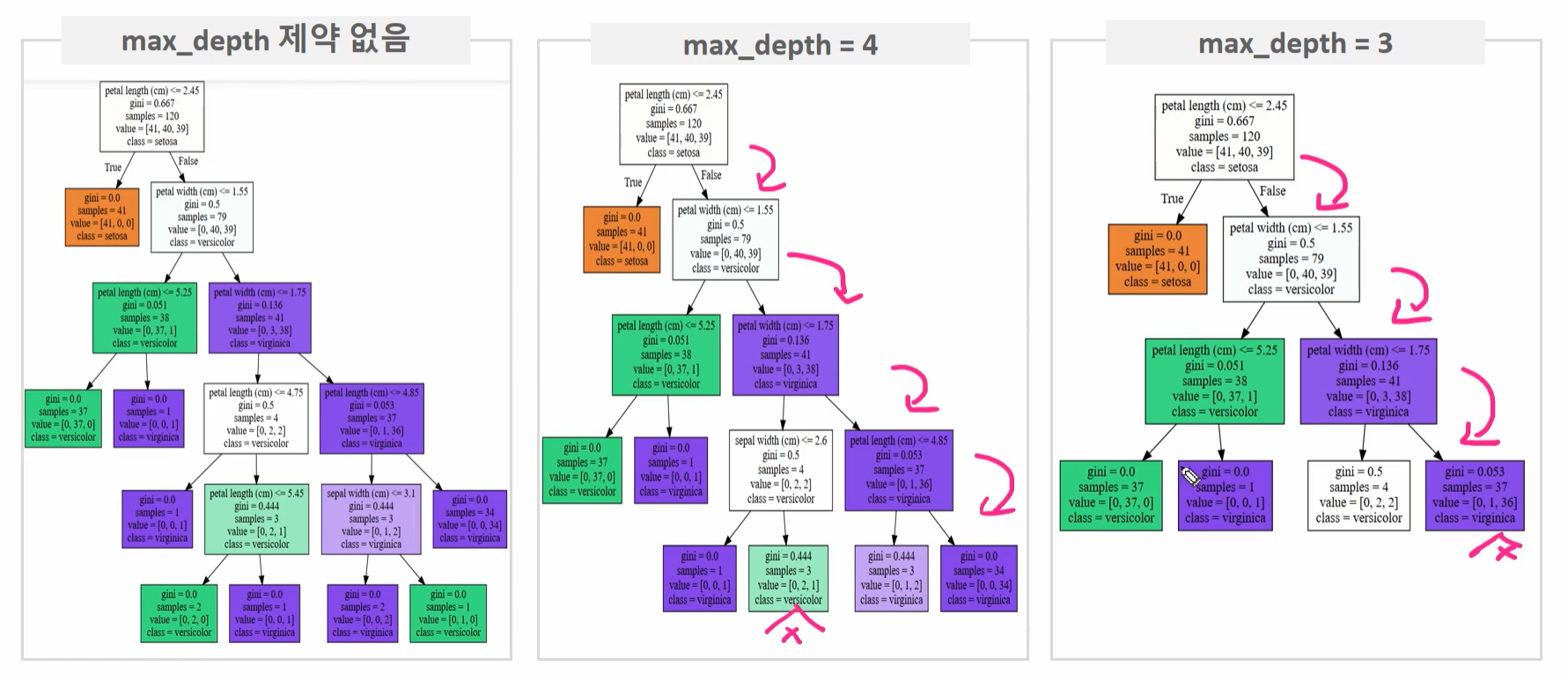
max_depth

- 트리의 최대 깊이

- None으로 설정하면 계속 분할함 → 노드가 가지는 데이터 개수가 min_samples_split보다 작아질 때까지 계속 깊이를 증가시킴

max_depth

 

max_features

- 최대 피처의 개수를 제한

- int형 -> 피처의 개수 / float형 -> 전체 피처 중 대상 피처의 퍼센트

- 디폴트: None

 

 

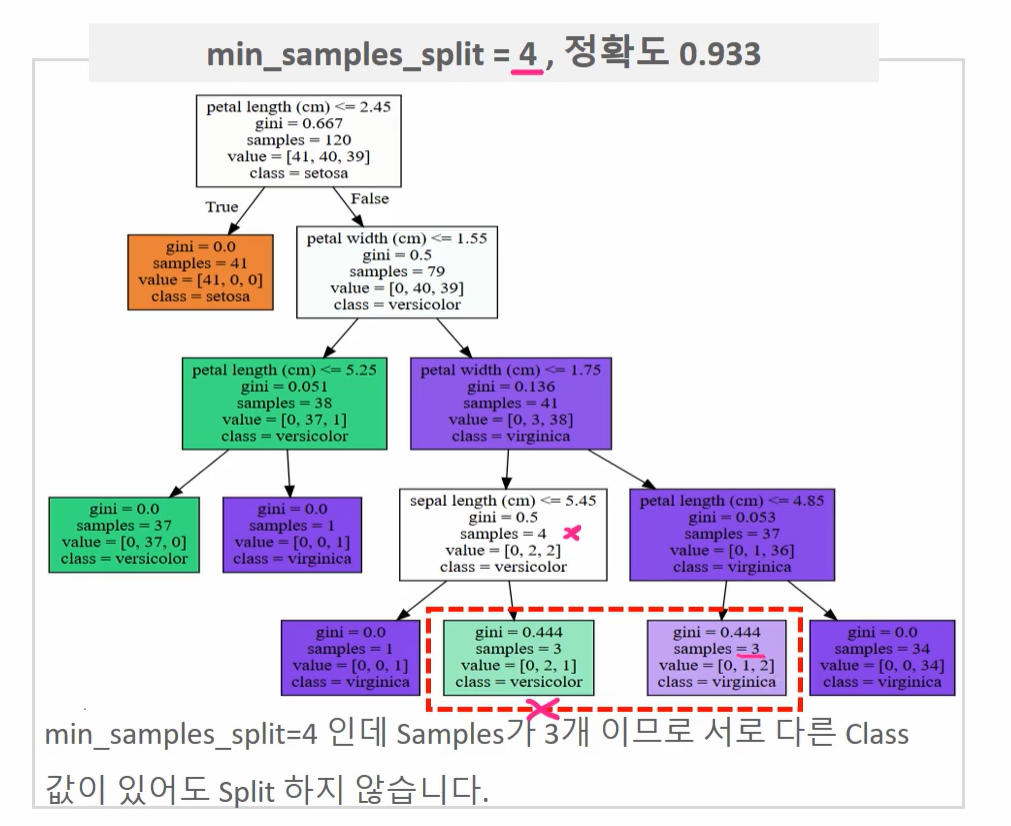
min_samples_split

- 노드를 분할하기 위한 최소한의 샘플 데이터 수 (과적합 제어에 사용됨)

- 디폴트: 2 (작게 설정할수록 분할되는 노드가 많아져서 과적합 가능성이 증가함

min_samples_split

 

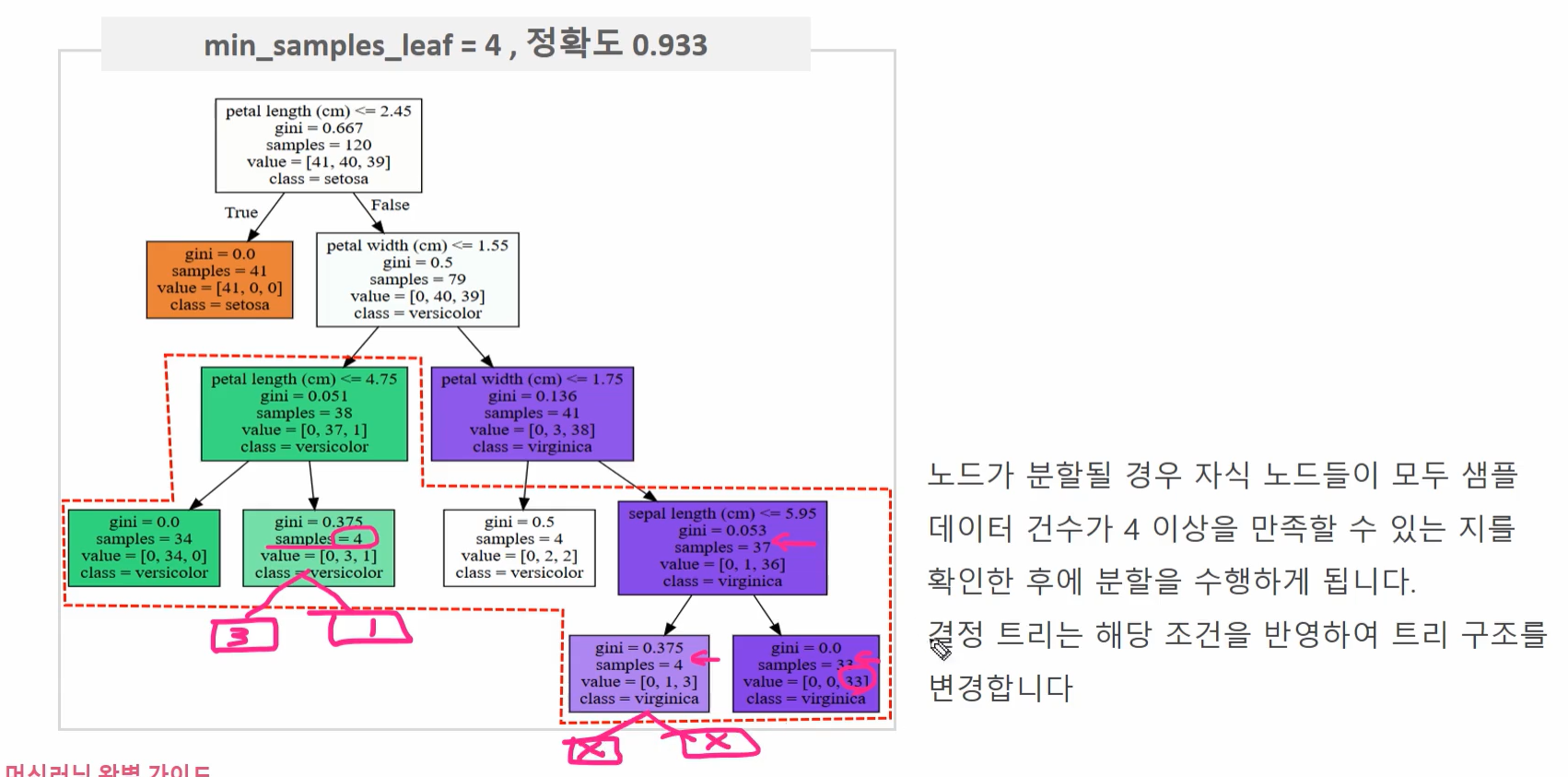
min_samples_leaf

- 분할이 될 경우 왼쪽과 오른쪽의 브랜치 노드에서 가져야 할 최소한의 샘플 데이터 수

- 값을 크게하면 분할이 어려움

 

- 노드가 분할될 경우 자식 노드들이 모두 샘플 데이터 건수가 4 이상을 만족할 수 있는지를 확인한 후 분할하게 됨

 

 

max_leaf_nodes

- 말단 노드의 최대 개수

 

 

(더 자세한 내용은 아래 표 참고)

 

→ max_depth 말고는 거의 다 과적합 제어를 위해 쓰임

 

[예제는 4.2 결정트리]

 

 

 

결정트리 피처 중요도의 이해

 

 

중요도

- dt_clf.feature_importances_ 이용

 

import seaborn as sns
import numpy as np
%matplotlib inline

# feature importance 추출!!!! 중요도! -> 기준: 분할을 얼마나 잘 하냐 (분할을 잘 한다고 엄청나게 좋기만 한 건 아님)
print("Feature importances:\n{0}".format(np.round(dt_clf.feature_importances_, 3)))

# feature별 importance 매핑
for name, value in zip(iris_data.feature_names , dt_clf.feature_importances_):
    print('{0} : {1:.3f}'.format(name, value))

# feature importance를 column 별로 시각화 하기 
sns.barplot(x=dt_clf.feature_importances_ , y=iris_data.feature_names)

결과

Feature importances:
[0.025 0.    0.555 0.42 ]
sepal length (cm) : 0.025
sepal width (cm) : 0.000
petal length (cm) : 0.555
petal width (cm) : 0.420

 

 

 

 

 

결정트리 과적합의 이해

 

 

결정 트리 과적합

 

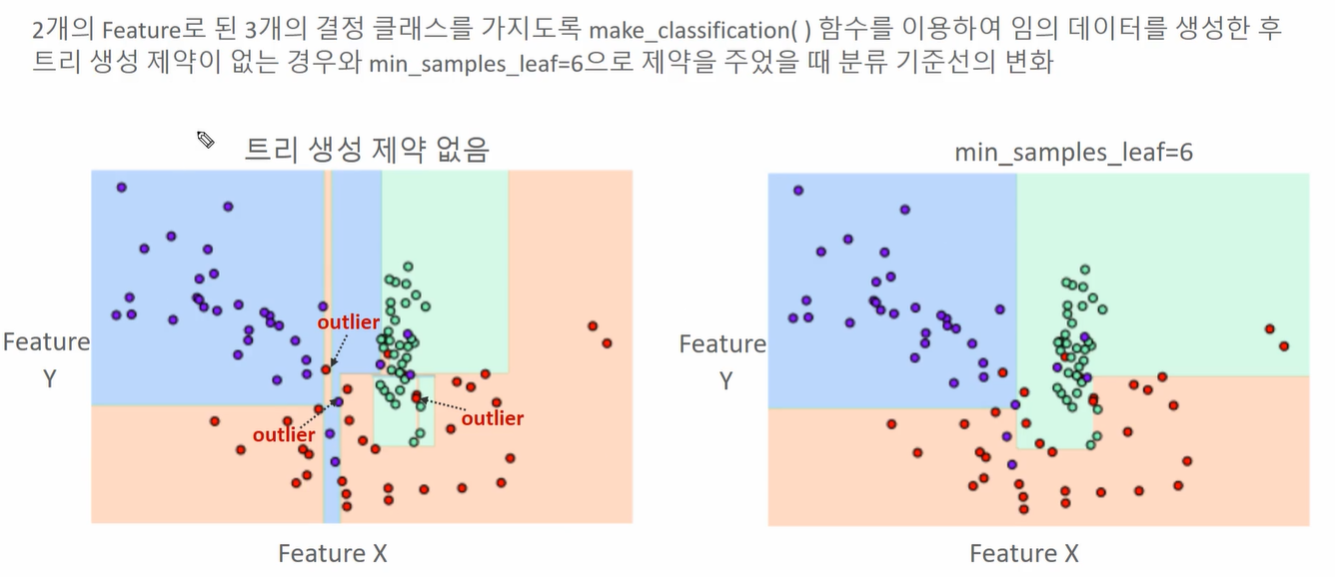
- 왼쪽보다 오른쪽이 훨씬 과적합에 영향을 받지 않는 분류 기준선임

- 트리 생성 제약이 없을 경우 outlier에 의해 과적합이 발생함

- 물론 왼쪽이 더 좋을 수도 있지만, test data의 입장에서 생각했을 때는 오른쪽이 더 낫다

- 머신러닝은 Underfitting보다 Overfitting이 더 문제다