열심히 코딩 하숭!
3. 처음 시작하는 머신러닝 | 파이토치 딥러닝 프로그래밍 본문
3. 처음 시작하는 머신러닝
3.3~4 경사 하강법 이해하기
1) 경사 하강법
- 가장 작은 손실(최솟값)을 구하기 위해 손실의 경사(기울기)를 따라서 파라미터 값을 수정해 나가며 효율적으로 손실이 최소가 되는 지점을 구하는 방법
- 예측 계산: 예측값 Yp를 구한다 (W, B 값의 변화에 따라 예측값도 변한다)
- 손실 계산: Yp와 Y의 차이를 구한다 (평균 제곱 오차 MSE)
- 경사 계산: 예측 함수를 구성하는 W, B의 값을 조금씩 바꿔가며, 그때 변화한 손실의 정도를 살펴본다
- 파라미터 수정: 경삿값에 작은 정수(학습률) Ir을 곱해서, 그 값만큼 W와 B를 동시에 줄여나간다
3.4~12 경사 하강법 구현하기
1) 데이터 전처리 | 데이터 변환 | 예측 계산
# 샘플 데이터 선언
sampleData1 = np.array([
[166, 58.7],
[176.0, 75.7],
[171.0, 62.1],
[173.0, 70.4],
[169.0,60.1]
])
print(sampleData1)
# x, y 선언
x = sampleData1[:,0] # 신장을 변수 x로
y = sampleData1[:,1] # 체중을 변수 y로
# 데이터 변환 (경사 하강법이 수월해지도록)
X = x - x.mean()
Y = y - y.mean()
# X, Y를 텐서 변수로 변환
X = torch.tensor(X).float()
Y = torch.tensor(Y).float()
# W, B 초기화
W = torch.tensor(1.0, requires_grad=True).float()
B = torch.tensor(1.0, requires_grad=True).float()
# 예측 함수
def pred(X):
return W * X + B
Yp = pred(X)
# 예측 값 Yp의 계산 그래프
params = {'W': W, 'B': B}
g = make_dot(Yp, params=params)
display(g)
- Yp에 대해 W, B를 입력으로 하는 계산 그래프

2) 손실 계산
# 손실 함수
def mse(Yp, Y):
loss = ((Yp - Y)**2).mean()
return loss
# 손실 계산
loss = mse(Yp, Y)
# 손실 계산 그래프 출력
params = {'W': W, 'B': B}
g = make_dot(loss, params=params)
display(g)

3) 경사 계산
# 손실에 대한 W와 B의 경사 계산
loss.backward()
# 경삿값 확인
print(W.grad)
print(B.grad)
# 학습률 정의
lr = 0.001
# 경사를 기반으로 파라미터 수정
# with torch.no_grad() 작성 필요
with torch.no_grad():
W -= lr * W.grad
B -= lr * B.grad
# 계산이 끝난 경삿값을 초기화함
W.grad.zero_()
B.grad.zero_()
# 파라미터 경삿값 확인
print(W)
print(B)
print(W.grad)
print(B.grad)
## 결과 ##
tensor(1.0190, requires_grad=True)
tensor(0.9980, requires_grad=True)
tensor(0.)
tensor(0.)
4) 반복 계산
# 초기화
# W와 B를 변수로 사용
W = torch.tensor(1.0, requires_grad=True).float()
B = torch.tensor(1.0, requires_grad=True).float()
# 반복 횟수
num_epochs = 500
# 학습률
lr = 0.001
# history 기록을 위한 배열 초기화
history = np.zeros((0, 2))
# 루프 처리
for epoch in range(num_epochs):
# 예측 계산
Yp = pred(X)
# 손실 계산
loss = mse(Yp, Y)
# 경사 계산
loss.backward()
with torch.no_grad():
# 파라미터 수정
W -= lr * W.grad
B -= lr * B.grad
# 경삿값 초기화
W.grad.zero_()
B.grad.zero_()
# 손실 기록
if (epoch %10 == 0):
item = np.array([epoch, loss.item()])
history = np.vstack((history, item))
print(f'epoch = {epoch} loss = {loss:.4f}')
5) 결과 평가
# 최종 파라미터 값
print('W = ', W.data.numpy())
print('B = ', B.data.numpy())
# 손실 확인
print(f'초기상태 : 손실:{history[0,1]:.4f}')
print(f'최종상태 : 손실:{history[-1,1]:.4f}')
## 결과 ##
W = 1.820683
B = 0.3675114
초기상태 : 손실:13.3520
최종상태 : 손실:4.6796
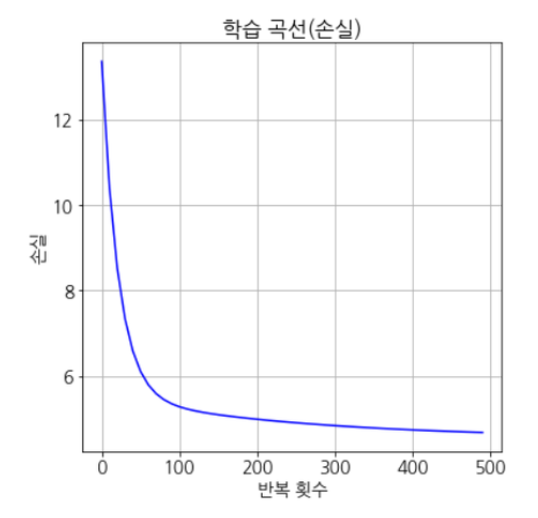
# 학습 곡선 출력(손실)
plt.plot(history[:,0], history[:,1], 'b')
plt.xlabel('반복 횟수')
plt.ylabel('손실')
plt.title('학습 곡선(손실)')
plt.show()
# x의 범위를 구함(Xrange)
X_max = X.max()
X_min = X.min()
X_range = np.array((X_min, X_max))
X_range = torch.from_numpy(X_range).float()
print(X_range)
# 이와 대응하는 예측값 y를 구함
Y_range = pred(X_range)
print(Y_range.data)
# y좌표와 x좌표 값 계산
x_range = X_range + x.mean()
yp_range = Y_range + y.mean()
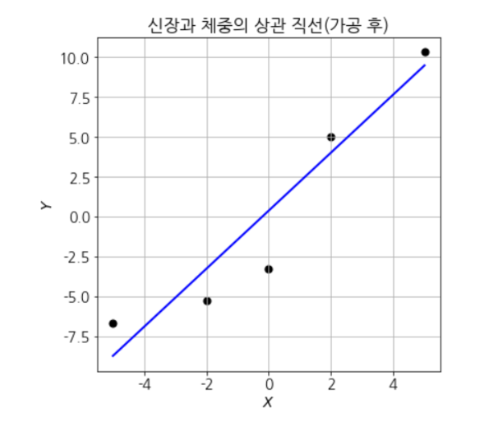
# 그래프 출력
plt.scatter(x, y, c='k', s=50)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.plot(x_range, yp_range.data, lw=2, c='b')
plt.title('신장과 체중의 상관 직선(가공 전)')
plt.show()
6) 최적화 함수
- optimizer ← 최적화 함수
# optimizer 로 SGD(확률적 경사 하강법)을 사용
import torch.optim as optim
optimizer = optim.SGD([W, B], lr=lr)
- 학습 코드에서 반복 계산을 아래와 같이 사용하면 된다
# 루프 처리
for epoch in range(num_epochs):
# 예측 계산
Yp = pred(X)
# 손실 계산
loss = mse(Yp, Y)
# 경사 계산
loss.backward()
**# 파라미터 수정
optimizer.step()
# 경삿값 초기화
optimizer.zero_grad()**
# 손실 기록
if (epoch %10 == 0):
item = np.array([epoch, loss.item()])
history = np.vstack((history, item))
print(f'epoch = {epoch} loss = {loss:.4f}')
💡 기본 컨셉 잘 복습하고 응용할 때 헷갈리지 말자!!
'프로그래밍 책 > 파이토치 딥러닝 프로그래밍' 카테고리의 다른 글
| 9. CNN을 활용한 이미지 인식 | 파이토치 딥러닝 프로그래밍 (1) | 2024.04.21 |
|---|---|
| 8. MNIST를 활용한 숫자 인식 | 파이토치 딥러닝 프로그래밍 (1) | 2024.04.21 |
| 4. 예측 함수 정의하기 | 파이토치 딥러닝 프로그래밍 (1) | 2024.04.17 |
| 2. 파이토치의 기본 기능 | 파이토치 딥러닝 프로그래밍 (0) | 2024.04.16 |
| 1. 딥러닝에 꼭 필요한 파이썬의 개념 | 파이토치 딥러닝 프로그래밍 (0) | 2024.04.15 |




