열심히 코딩 하숭!
우선순위큐 & 힙 | 자료구조실습 2주차 과제 본문
* 성신여대 22-2학기 자료구조실습 수업시간에 배운 내용을 토대로 요약 정리한 글입니다
1. 우선순위큐 & 힙
1-1. 우선순위큐 (priority queue)
정의
- 우선순위가 가진 요소들을 저장하는 큐
- 우선 순위가 높은 데이터가 먼저 나가게 됨
구현 방법
1) 배열을 이용 (오름차순)

<소요 시간>
- 삽입: O(1)
- 삭제: O(n)
=> 오래 걸림
2) 연결리스트 (내림차순)

<소요 시간>
- 삽입: O(n)
- 삭제: O(1)
=> 오래 걸림
3) 힙을 이용한 구현
- 완전이진트리를 이용한 우선순위큐 구현
- 일종의 반 정렬 상태를 유지
<소요 시간>
- 삽입: O(logn)
- 삭제: O(logn)
=> 비교적 효율적! 1) 2)보다 훨씬 유리하다
그렇다면 힙에 대해 더 자세히 알아보자!
1-2. 힙 (heap)
정의
- 부모 노드가 자식 노드보다 크거나 (혹은 작거나) 같은 완전 이진트리
- maxHeap(최대 힙): (부모 노드 키값) >= (자식 노드 키값)
- minHeap(최소 힙): (부모 노드 키값) <= (자식 노드 키값)

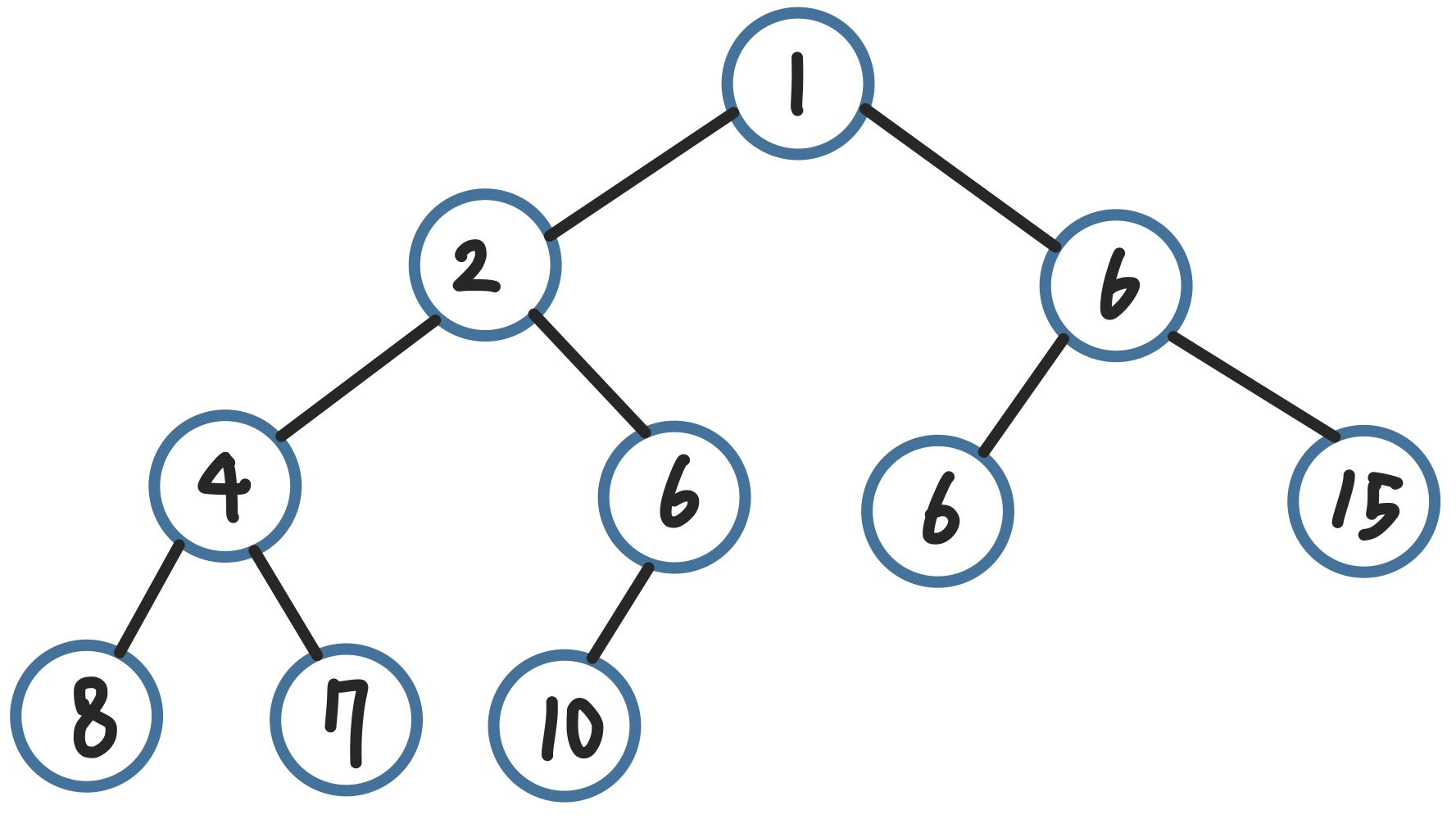
* 같은 레벨에 있는 노드들끼리는 순서 상관 X!!!! (부모 노드와의 관계가 중요함)
구현 방법
- 힙의 개념은 완전이진트리로 나타내고 / 실제 구현은 배열을 이용한다
<예시>
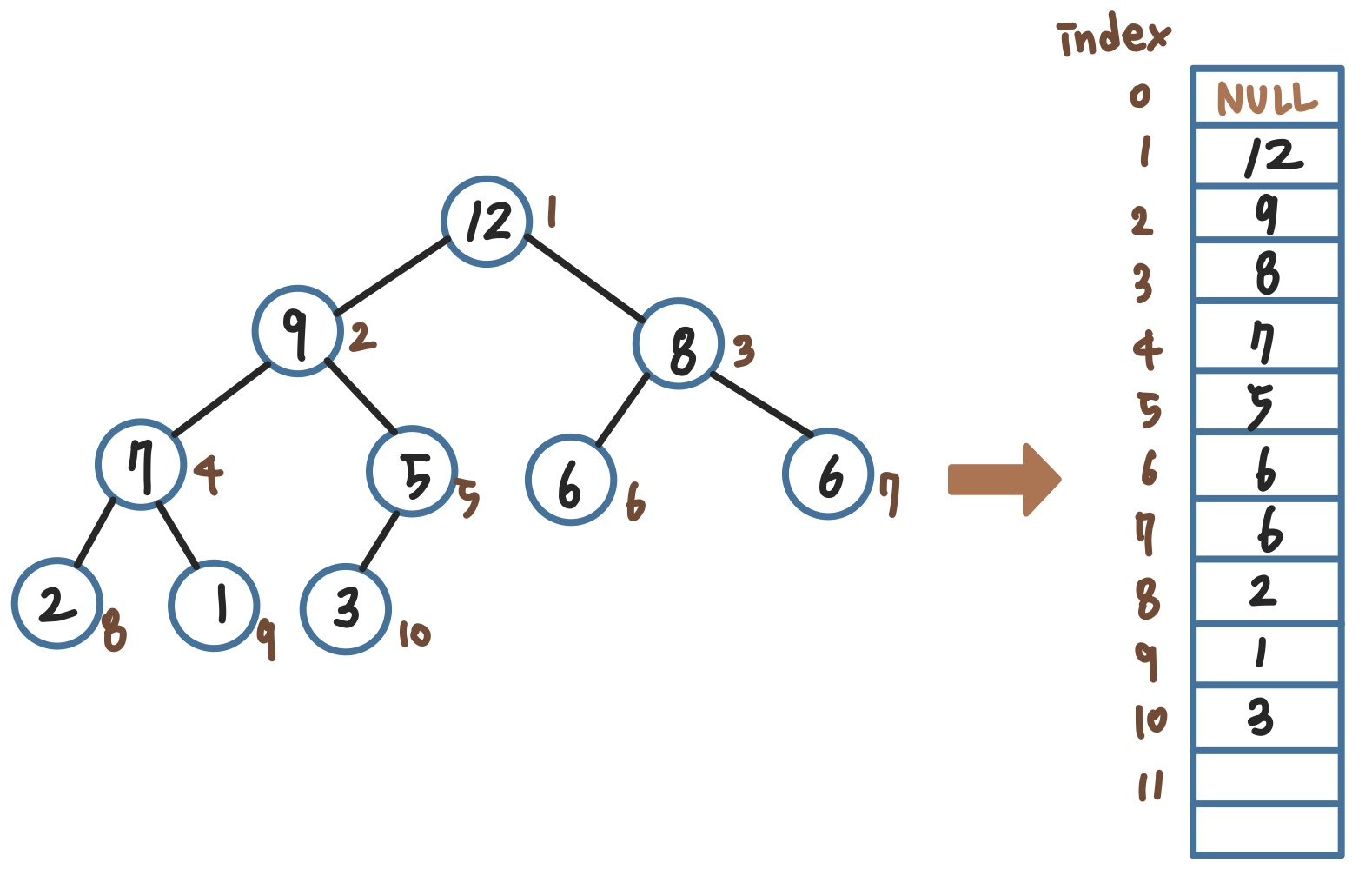
배열 사용 시 특징
1) 구현을 쉽게 하기 위해 첫번째 인덱스인 0은 사용하지 않는다
2) (왼쪽 자식 노드의 인덱스) = (부모 노드의 인덱스) * 2
3) (오른쪽 자식 노드의 인덱스) = (부모 노드의 인덱스) * 2 + 1
4) (부모 노드의 인덱스) = (자식 노드의 인덱스) / 2
<예시>

2. C++을 이용한 우선순위큐 프로그래밍 방법 (MaxHeap을 기준으로)
2-1. 전체 구조
우선순위큐 프로그래밍을 위해 두 가지 class를 생각해볼 수 있다.
- HeapNode class - 힙에 저장할 노드 클래스
- MaxHeap class - 노드들을 배열에 저장하여 우선순위큐를 구현하는 최대 힙 클래스
먼저 두 가지 클래스의 생김새를 살펴보자.
HeapNode
class HeapNode {
int key; // 노드의 key 값
public:
HeapNode(int k = 0) : key(k) { } // 생성자를 통해 멤버변수 key값 초기화
void setKey(int k) { key = k; }
int getKey() { return key; }
void display() { cout << key; }
};1) key값: 노드의 우선순위를 결정하는 값
2) 생성자 호출 시 우선 key값을 0으로 초기화
3) setKey, getKey 함수를 통해 key값을 설정하고 return함
4) display 함수를 통해 key 값을 보여줌
MaxHeap
#define MAX_ELEMENT 200
class MaxHeap {
HeapNode node[MAX_ELEMENT]; // HeapNode들이 들어가있는 배열
int size; // MaxHeap의 HeapNode 개수
public:
MaxHeap() : size(0) { } // 생성자: size를 0으로 초기화
bool isEmpty() { return size == 0; } // node가 아예 없을 경우
bool isFull() { return size == MAX_ELEMENT - 1; } // 배열이 node로 꽉 찼을 경우
HeapNode& getParent(int i) { return node[i / 2]; } // (부모노드 인덱스) = (자식노드인덱스) / 2
HeapNode& getLeft(int i) { return node[i * 2]; } // (왼쪽자식노드 인덱스) = (부모노드 인덱스) * 2
HeapNode& getRight(int i) { return node[i * 2 + 1]; } // (오른쪽자식노드 인덱스) = (부모노드 인덱스) * 2 + 1
void insert(int key) { /* 생략 */ } // 밑에서 설명
HeapNode remove() { /* 생략 */ } // 밑에서 설명
HeapNode find() { return node[1]; } // Heap에서 0 인덱스는 비워두므로 node[1]부터 시작임
};
1) HeapNode node[MAX_ELEMENT]: HeapNode들이 들어가있는 배열
- 힙의 개념은 완전이진트리이지만 코드 작성 시 이를 배열로 구현하기 때문에 배열을 멤버 변수로 선언해야 함
2) get 함수 구현
(부모노드 인덱스) = (자식노드인덱스) / 2
(왼쪽자식노드 인덱스) = (부모노드 인덱스) * 2
(오른쪽자식노드 인덱스) = (부모노드 인덱스) * 2 + 1
3) Heap에서 0 인덱스는 비워두므로 find 함수에서 return값으로 node[1]을 반환해야 함
4) insert(삽입)와 remove(삭제) 함수는 아래에서 더 자세히 다뤄보자.
2-2. 삽입 & 삭제 연산
삽입 (insert)
삽입의 경우
UpHeap을 이용하면 된다
<순서>
1> 우선 새로운 노드가 들어오면 heap의 제일 마지막 노드에 이어서 삽입한다.
2> 삽입한 후 새로운 노드를 부모 노드들과 비교 후 교환하며 힙의 성질을 만족하도록 만든다.
3> 이때, 힙의 성질이란? MaxHeap의 경우 (부모 노드의 key값)이 (자식 노드의 key값)보다 크거나 같아야 함
<예시>
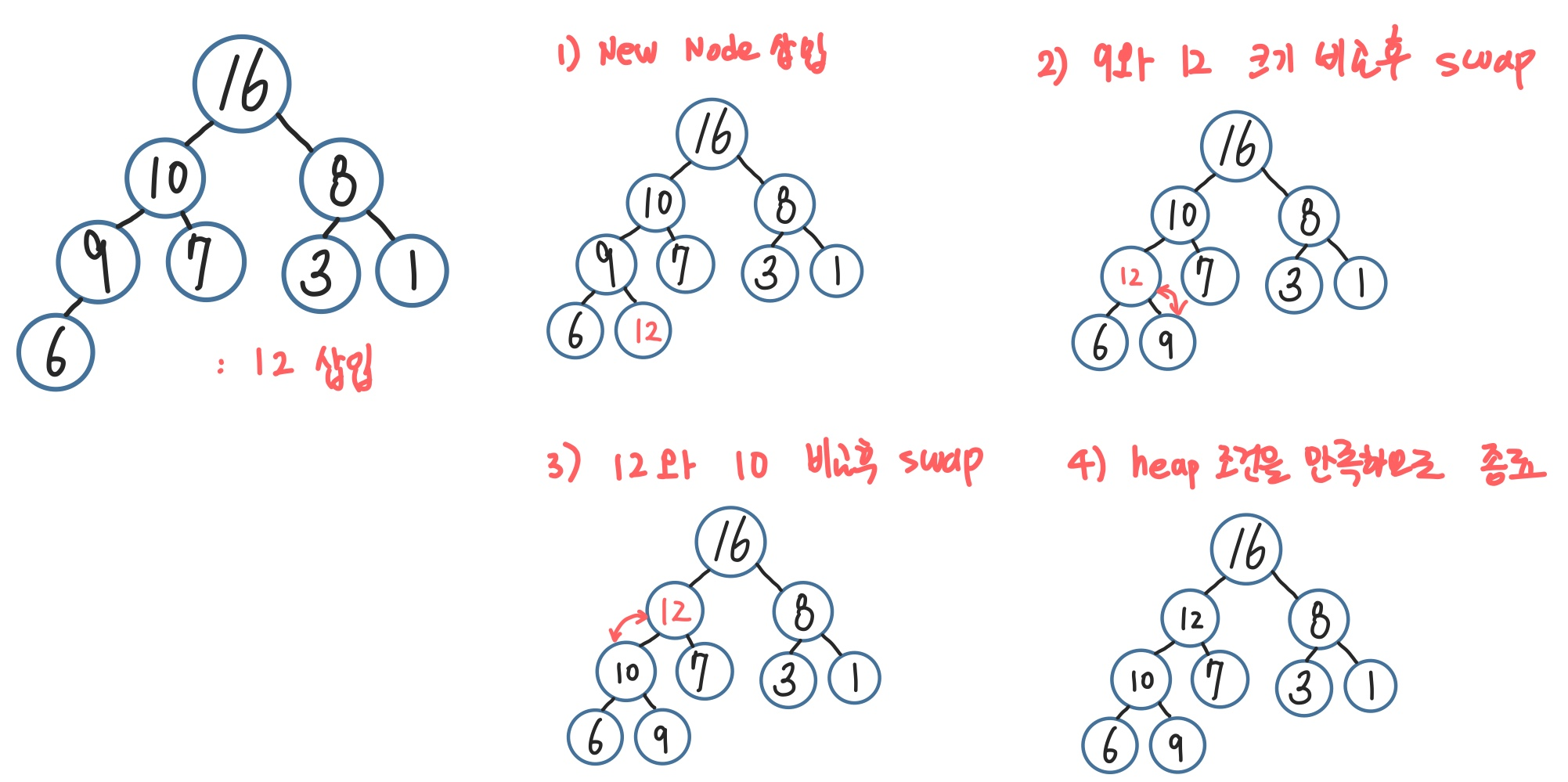
<구현>
void insert(int key) {
if (isFull()) return; // 힙이 가득차서 insert를 할 수 없는 경우
int i = ++size; // 새로운 노드가 insert될 곳의 인덱스
while ((i != 1) && (key > getParent(i).getKey())) {
// while: i가 루트(인덱스 1)가 아니고
// 새로운 노드의 key값이 부모 노드의 key 값보다 클 경우
// 부모와 자식을 swap
node[i] = getParent(i); // 현재 자식 노드에 부모 노드를 삽입하고
i /= 2; // i 인덱스를 2로 나누어주어 부모 노드의 위치였던 한 레벨 위로 상승
}
node[i].setKey(key); /// 최종으로 i 인덱스 자리에 새로운 노드를 삽입
}1) while문의 조건: i가 루트가 아니어야 하고 새로 삽입할 노드의 key값이 부모 노드의 key값보다 커야 한다.
2) 부모 노드와 자식 노드를 swap하는 과정: 우선 i 인덱스 자리에 부모 노드였던 HeapNode를 삽입하고, 다시 while문 조건을 검사하기 전에 i /= 2를 해주어 i 를 부모의 자리로 올린다.
삭제 (remove)
삭제의 경우
DownHeap을 이용하면 된다
<순서>
1) 루트 노드를 삭제한다
2) 마지막에 있는 리프 노드를 루트 노드의 자리로 옮긴다
3) 루트 노드부터 말단 노드까지 경로에 있는 노드들의 key 값을 비교하고 교환하여 heap 성질을 만족시킨다
<예시>
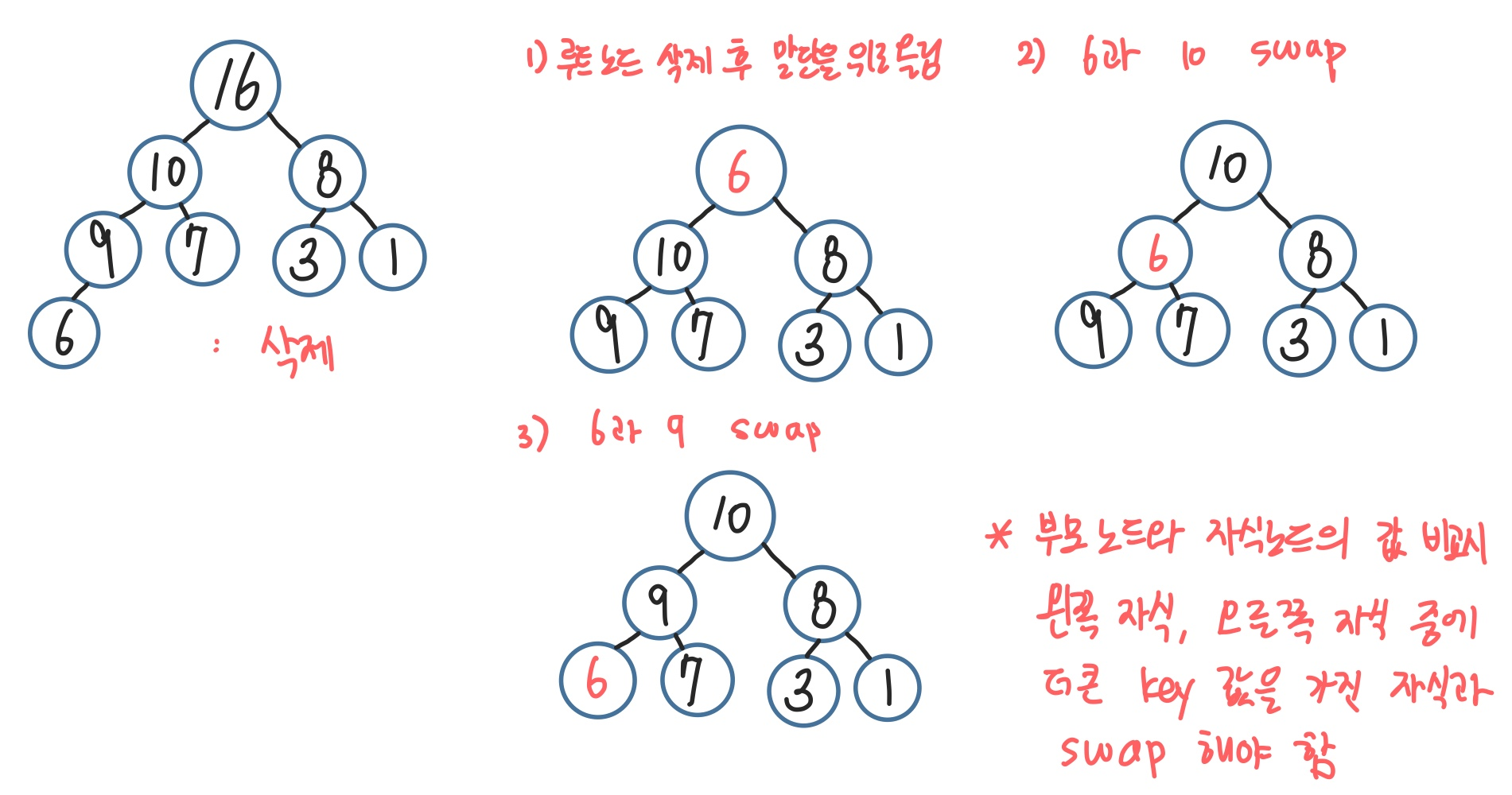
<구현>
HeapNode remove() {
if (isFull()) error(); // 힙이 비어서 remove를 할 수 없는 경우
HeapNode item = node[1]; // 루트 노드 (remove후 return할 대상)
HeapNode last = node[size--]; // 현재 힙의 마지막에 위치한 노드
int parent = 1; // 마지막 노드의 위치를 루트로 생각함
int child = 2; // 루트의 왼쪽 자식 인덱스
while (child <= size) {
// 왼쪽 노드와 오른쪽 노드의 key값을 비교하여 더 큰 값을 가진 노드를 child로 선언
if (child < size && getLeft(parent).getKey() < getRight(parent).getKey())
child++;
// 마지막 노드의 값이 자식 노드보다 크거나 같을 경우 heap 조건을 만족하므로 while문 종료
if (last.getKey() >= node[child].getKey()) break;
// 한 단계 아래로 이동
node[parent] = node[child];
parent = child;
child *= 2;
}
node[parent] = last; // 마지막 노드를 최종 위치에 저장
return item; // 루트 노드 반환
}
1) 인덱스를 담는 parent와 child 값을 두고 말단 노드와 하나씩 크기를 비교해가며 위치를 수정함
2) 마지막에 저장해두었던 루트 노드를 return 하면서 마무리
2-3. 힙 정렬
힙을 이용해 정렬을 할 경우,
한 번에 하나씩 요소를 힙에서 remove하여 저장하면 된다
void heapSort(int a[], int n) {
MaxHeap h;
// 넘어온 배열 a의 값들을 하나씩 h에 넣어줌
for (int i = 0; i < n; i++) {
h.insert(a[i]);
}
// h에서 값을 하나씩 remove함. 이때 가장 큰 값부터 반환 됨
// 오름차순 정렬을 위해 a[n-1]에서 부터 값을 넣음
for (int i = n - 1; i >= 0; i--) {
a[i] = h.remove().getKey();
}
}
아래는 STL을 이용한 방법
// 최대 힙 정렬
void MaxHeapSorting(int a[], int n) {
priority_queue <int> maxHeap; // maxheap 우선순위큐 객체 생성
for (int i = 0; i < n; ++i)
maxHeap.push(a[i]); // a 배열에 있는 값들을 maxHeap에 하나씩 삽입
for (int i = 0; i < n; ++i) {
a[i] = maxHeap.top(); // 가장 위에 위치하는 값(max값)을 저장
maxHeap.pop(); // 그 후 pop()해서 삭제
}
}
// 최소 힙 정렬
void MinHeapSorting(int a[], int n) {
priority_queue<int, vector<int>, greater<int>>minHeap; // minheap 우선순위큐 객체 생성
for (int i = 0; i < n; ++i)
minHeap.push(a[i]); // a 배열에 있는 값들을 minHeap에 하나씩 삽입
for (int i = 0; i < n; ++i) {
a[i] = minHeap.top(); // 가장 위에 위치하는 값(min값)을 저장
minHeap.pop(); // 그 후 pop()해서 삭제
}
}
2-4. 함수 정의

2-5. 우선순위 큐 STL
Heap 객체 생성
- 최대 힙 객체 생성
#include <queue>
priority_queue<int> maxHeap;
- 최소 힙 객체 생성
#include <queue>
#include <functional>
priority_queue<int,vector<int>,greater<int>> minHeap;자주 사용하는 STL
- pair class
- 두 개의 객체를 하나의 객체로 만든다
- 헤더: #include <utility>
- 선언: pair <[type 1], [type 2]> 객체이름;
- first: 객체의 첫번째 인자 반환 (우선순위큐와 사용 시 key값이 됨)
- second: 객체의 두번째 인자 반환 (우선순위큐와 사용 시 모든 key값이 동일 할 때 second가 key로 작용)
- tuple class
- 세 개의 객체를 하나의 객체로 만든다
- 헤더: #include <tuple>
- 선언: tuple<[type 1], [type 2], [type 3]> 객체이름;
- vector class
- 동적 배열, array 크기를 동적으로 할당할 수 있음
- 헤더: include <vector>
- 선언: vector<[type]> 객체이름;
- 사용: vec.push_back(5); / vec.pop_back();
3. 문제 풀이
3-1. 백준 1966번 - 프린터 큐
https://chaesoong2.tistory.com/4
1996번 프린터 큐 | baekjoon 문제 풀이
https://www.acmicpc.net/problem/1966 1966번: 프린터 큐 여러분도 알다시피 여러분의 프린터 기기는 여러분이 인쇄하고자 하는 문서를 인쇄 명령을 받은 ‘순서대로’, 즉 먼저 요청된 것을 먼저 인쇄한다
chaesoong2.tistory.com
3-2. 백준 1655번 - 가운데를 말해요
(시간 초과로 실패했지만, 일단 풀이를 올린 후 다음주 중으로 다시 풀어보겠습니다...!!! 아좌좌.)
https://chaesoong2.tistory.com/3
1655번 가운데를 말해요 | baekjoon 문제 풀이
https://www.acmicpc.net/problem/1655 1655번: 가운데를 말해요 첫째 줄에는 백준이가 외치는 정수의 개수 N이 주어진다. N은 1보다 크거나 같고, 100,000보다 작거나 같은 자연수이다. 그 다음 N줄에 걸쳐서 백
chaesoong2.tistory.com
'학교 과제 > 2022-2 자료구조실습 과제' 카테고리의 다른 글
| BFS vs DFS | 자료구조실습 9주차 과제 (0) | 2022.11.06 |
|---|---|
| 2022 하천 분리수거 마라톤 대회 '시뮬레이션 프로그램🏃' | Red Black Tree | 자료구조실습 중간과제 (0) | 2022.10.22 |
| AVL tree | 자료구조실습 4주차 과제 (0) | 2022.10.02 |
| 이진 탐색 트리 | 자료구조실습 3주차 과제 (0) | 2022.09.25 |
| 프로젝트를 위한 시각 넓히기 | The SDGs 2021을 읽고 | 14. 해양 생태계 (0) | 2022.09.12 |




